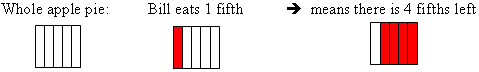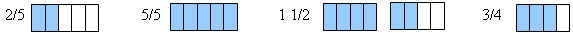Eating fractions of pie, pizza and cake

Eating fractions of pie, pizza and cake

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about adding and subtracting fractions.

a) Petra ate two-fifths (\(2 \over 5\)) of a pizza and Sarah ate one-fifth (\(1 \over 5\)). Show how to work out how much pizza they ate altogether.

 
 
 
 
 

Answer: __________  

b) Lima and Paul each had the same sized cake. Lima ate four-fifths (\(4 \over 5\)) of his cake and Paul ate three-fifths (\(3 \over 5\)) of his cake. Show how to work out how much cake they ate altogether.

 
 
 
 
 

Answer: __________  
 
c) Bill ate one-fifth (\(1 \over 5\)) of a whole apple pie. Show how to work out how much pie was left.
 
 
 
 
 

Answer: __________  

d) Andrew started with one and a half pizzas (1\(1 \over 2\)) and ate three-quarters (\(3 \over 4\)) of a whole pizza. Show how to work out how much pizza is left.

 
 
 
 
 

Answer: __________  

 

Task administration: 
This task is completed with pencil and paper only.
Levels:
3, 4
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Keywords: 
fractions, addition, subtraction
Description of task: 
Students answer questions involving adding and subtracting fractions of food.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Additive thinking, sets 6-7
Additive thinking, sets 7-8
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
    Y6 (11/07)
a) working involving adding 2/5 and 1/5 :

  • Use of fractional notation adding only the numerators; or
  • A diagram with a common referent whole showing 2/5 and 1/5 and adding them together, e.g.,

3/5

 easy

 

easy
b) working involving adding 4/5 and 3/5 :

  • Use of fractional notation adding only the numerators; or
  • A diagram with a common referent whole showing 4/5 and 3/5 and adding them together, e.g.,

7/5 or 12/5

 moderate

difficult
c) working involving subtracting 1/5 from a whole:

  • Use of fractional notation subtracting only the numerators; or
  • A diagram with a common referent whole showing 4/5 and 3/5 and adding them together, e.g.,

4/5

 easy

 

easy
d) working involving subtracting 3/4 from 11/2 :

  • Use of fractional notation subtracting only the numerators; or
  • A diagram with a common referent whole showing 4/5 and 3/5 and adding them together, e.g.,

3/4

 moderate

 

 

moderate

Based on a representative sample of 167 students.

NOTE:  Other shapes can also be used: many students used circles, which are harder to show equal parts and can actually be a barrier to accurate representation.

Diagnostic and formative information: 
  Common error Likely misconception
a)
b)
c)
d)		 3
7
4
3		 Whole number misconception about fractions – working with the pieces.
Only dealing with the numerator (number of pieces)
Students may also describe what they have added by writing "pieces" after the number.  This error was far more common in question b) where a third of students made this error compared with one-tenth in question a).
a)
b)		 3/10
7/10		 Whole number misconception about fractions
Students treat the fraction as two separate numbers – adding the top and bottom separately and then putting the sums of each top and bottom.
a)
b)		 13
17		 Whole number misconception about fractions
Students add all the numbers (top and bottom) together.
a)
b)		 4
8		 Whole number misconception about fractions
Students add all the numbers (top and bottom) together using a system of place value between the denominators and numerators. 
For example, in question a) the two denominators (5, 5) make 10.  The "1" is carried up and added to the 1+2 of the numerators (1+2+1=4).
a)-
d)		 Using a diagram that is not comparable – the size cannot be visually confirmed because:

  • the diagrams are too inaccurate to represent the fractions; or
  • the diagrams are different for each fraction (rectangle/circle); or
  • diagrams don't show any partitions or incomplete.
d) 3/6 or 1/2 Finding the fraction of a different referent whole
Students have worked out the fraction of all the pizza that has been eaten (i.e., half all the pizza that was there has been eaten) rather than fraction of a single pizza.

 

Next steps: 
Whole number misconceptions about fractions: understanding the part-whole relationship
Students who have any of the whole number misconceptions identified above need to develop a part-whole understanding of fractions before trying to devise a system to add or subtract fractions.  If required, students could go back to partitioning and explore constructing the parts (unit fractions), combining these parts to make non-unit fractions that are between 0 and 1 (also called proper fractions), and naming these new fractions (part-whole fractions).

Writing the number of pieces rather than the fraction
For students who gave the number of pieces as their answer, encourage them to find out what fraction the pieces are and incorporate that into their answer, e.g., question d) 3 pieces each of 1/4 is 3/4 .  Asking students what the whole shape is, and then what part they are finding, can support them to develop a more part-whole understanding about fractions.

Using diagrams to show how they added/subtracted the fractions
For students who constructed incomplete or inaccurate diagrams to show how to work out these fraction problems, ask students to explain how they know the diagram they have drawn accurately shows the fraction they need to use.  Then get them to explain or justify how the parts can be added or subtracted (because they are the same size, we can add/subtract fractions).
Students can be encouraged to use easier shapes to represent the fractions, e.g., rectangles can be easier to show (and compare) a range of fractions:

These fractions are then all fairly easily manipulated to solve the addition and subtraction problems using basic counting skills and an understanding of the unit fraction.

For students who showed their working using an accurate diagram, encourage them to look at other students' strategies to show or explain how they got their answer.  For example in question c) students could say
"I have a whole and want to take away 1/5 , I know that there are 5 fifths in a whole which means there is one left"  and for question d)
"I know that 3/4 is 1/2 and 1/4 , so to take 3/4 away from 11/2 , I take the half away which equals 1 and then a quarter from 1 and the answer is 3/4 because there are 4 quarters in 1."

Further exploration
These questions asked students to add and subtract fractions with simple and similar denominators.  It is also important to encourage students to explore other fractions (including improper fractions) using the strategies they have come up with.  This should help them develop more robust addition and subtraction strategies that may work for all fractions.

Strategies
Diagrams were used by about two-thirds of students for the addition problems, and about three-quarters for the subtraction problems.  Of these diagrams about two-thirds correct or accurate representations of the problem.  However, even correct diagrams had a mixed success rate with only about half of them leading to correct answers for b) and about two-thirds for d), and about 80-85% for questions c) and a).  This mixed success indicates that diagrams are not sufficient in themselves and should be backed up by explanation, justification, or at least labelling.  This can be scaffolded in whole class discussion where students share and critique their own and others' strategies to develop a fuller understanding.

Other resources

  • For similar ARB resources about adding and subtracting fractions, click on the link or use the keywords, fractions AND addition
  • Click on the link for further information about addition and subtraction of fractions.

Numeracy resources
Book 7: Teaching Fractions, Decimals and Percentages, 2006:
Hungry birds, (p.11), Advanced counting/ Early additive part-whole.