Estimating multiplication
Estimation is an approximate answer you can easily work out without calculating the exact numbers.
| a) |
8 students each have about 23 pens in their pencils cases.
Show what you did to estimate how many pens there are altogether.
|
|
|
||
| b) |
There are 12 friends who have about 27 Dragonball Z cards each.
Show what you did to estimate how many cards there are altogether.
|
|
|
||
| c) |
94 students have about 56 marbles each.
Show what you did to estimate how many marbles there are altogether.
|
|
|
||
| d) |
241 students have about 37 Pokemon cards.
Show what you did to estimate about how many stickers there are altogether.
|
|
|
| Y8 (10/2010) | ||
| a) |
Any tidy number between 160 and 230 [Do not accept 184 unless the student uses an estimation method followed by exact compensation that can easily be done mentally.1] Working that involves any of the following estimation methods:
Possible compensations3:
|
moderate moderate |
| b) |
Any 1 of: 200, 400 or any tidy number between 240 and 360 [Do not accept 324 unless the student uses an estimation method followed by exact compensation that can easily be done mentally.1] Working that involves any of the following estimation methods:
Possible compensations3:
|
difficult moderate |
| c) |
Any tidy numbers between 4500 and 6000 [Do not accept 52644 or numbers close to it such as 5260, 5270 or 5300, as the student has probably done an exact calculation then rounded it.] Working that involves any of the following estimation methods:
Possible compensations
|
very difficult moderate |
| d) |
Any 1 of: 6000, 10 000, or any multiples of 100 between them. [Do not accept 89174 or numbers close to it such as 8900, 8910, or 8920, as the student has probably done an exact calculation then rounded it.] Working that involves any of the following estimation methods:
Possible compensations3:
|
very difficult difficult |
NOTES:
- Accept if exact compensations are made in parts a) and b).
- We include 25, 250 etc. as tidy numbers along with 10s, 100s, 100s, etc.
- Accept any estimation even if no compensations were made.
- If an exact answer is given student is unlikely to be using estimation strategies especially in parts c) and d).
- Do not accept strategies where the student needs to perform some multiplications manually.
For more information, including descriptions of the different methods (e.g., front-end etc.) click on Computational estimation concept map.
- The first step for these estimations is to evaluate the order of magnitude of the answer, e.g., is 241 - 37 in the 10s, 100s, 100s, 10 000s or 100 000s?
- The next step is reformulation. This changes the original numbers to ones which give an answer that is close to the exact one, but can be performed much more easily, preferably mentally.
- After the first step, students may make a final compensation. This adjusts the first estimate to a closer estimate. Many students who scored highly in our sample did not make a final compensation even though it was possible. It is useful to just estimate the compensation (e.g., in part c), 94 * 56 = 100 * 56 but this is too big by about 6 x 50 = 300).
- Other students reformulated the problem so no compensation was needed (e.g., 12 * 27 is close to 10 * 30) because one number has increased and the other decreased. This is called intermediate compensation.This is most effective if students are proportional thinkers. They should consider the relative shifts that their compensation entail rather than the absolute (additive) shifts. For example, if the student is estimating 94 * 56 and takes 94 up to 100, that is about a 6% increase. They should therefore decrease 56 by about 6%, i.e. by about 3 down to 53. An estimate of 100 x 53 = 5300 is a closer that an estimate of 100 * 56 = 5600. Alternatively, since 94 is about twice 56, so increasing 94 by 6 is more accurately offset by decreasing 56 by half of 6, i.e., 3. This proportional adjustment becomes more important if the numbers are of different orders of magnitude. So for 241 * 37, 240 * 40 = 9600 is not nearly as close an estimate as 200 x 43 = 8600 (i.e., drop 241 by about a sixth to 200, so increase 37 by about a sixth to 43).
Click on the link Analysis of students responses [pdf] for the most common student responses.
Prior knowledge needed
- A firm base of multiplicative facts to 10 x 10.
- Good place value concepts, particularly the effect of multiplying numbers by 10, 100, 1000 (e.g. 20 x 40 = 800)
- It is essential that the students are comfortable with the concept of computational estimation (getting answers that are close to the real answer using mental computational strategies).
| Common response | Likely misconception | |
|
a) b) c) d) |
184 864 5264 8917 |
Exact calculation These students do an exact calculation. This will be easy to see from the working that they give. Often this will be a vertical algorithm. Some of these students work from the largest cross-product to the smallest, e.g., 12 × 27 = (10 × 20) + (10 × 7) + (2 × 20) + (2 × 7). This starts off with the front-end estimation of 10 × 20 = 200. The first-order compensations of (10 × 7) + (2 × 20) updates this to 200 + 70 + 40 = 310, which some students can do mentally. |
|
b) c) |
214 [(10 x 20) + (2 x 7)] 4524 (or 474) [(90 x 50) + (4 x 6)] |
Exact calculation with missing cross-over elements These students multiply the tens digits together and the ones digits but not the "cross-over" elements (i.e., tens with ones and vice versa). With 474 this is coupled with a order of magnitude error (i.e., 90 × 50 = 450, instead of 4500). |
|
a) b) c) d) |
190 (180) 860 or 870 5260, 5270 or 5300 8900, 8910 or 8920 |
Exact calculation followed by rounding These students do an exact calculation but then round their answer. They realise that an estimate is not exact, and so round their result to a tidy number close to their calculation 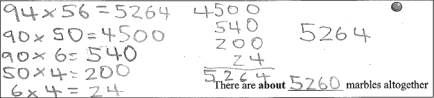 This student clearly used place value decomposition, but then rounded their answer. |
|
c) d) |
450, 500, 540, 560, 600 etc. 600, 700, 720, 800, 960, 1000 etc |
Miscalculates by a factor of 10 (often too small), e.g., 94 × 50 = 470 |
|
b) c) |
200, 400 etc. 4500, 6000 etc. 6000, 8000, 10 000 etc. |
Does not use compensation These students do not attempt to do a simple adjustment of their answer when it is possible. This is particularly common if just one number is rounded or when front-end estimation is used. In the latter it is easy to see that the answer is always too small. For example, for 241 × 37, 240 × 30 = 7200 is clearly too small. Adding on 200 × 3 or 240 × 3 gives a much closer estimate. |
|
a) b) c) d) |
10 × 21 10 × 29 90 × 60 or 100 × 50 240 × 38 |
Compensates "additively" The student comments how they have added on and taken away the same amount (2)  Students making this error will believe that their answer is very close to the exact answer. |
Exact calculation or Exact calculation followed by rounding or Exact calculation with missing
cross-over elements
These students need to realise that an answer that is close to the exact one can be obtained by performing simple mental computations. These are most often related to basic facts that the students already have. For more information about estimation, click on the link Computational estimation concept map. Get students doing quick fire estimates such as: "What is 8 × 54 approximately?"; "What is 13 x 64 approximately?" etc. Shortening the time frame or making the numbers larger will push the students towards estimation rather than exact calculation.
Miscalculates by a factor of 10 (often too small)
The first question students should ask themselves when estimating should be "Is the answers in the 10s, 100s, 1000s, 10 000s etc.?" In fact, you should ask this every time you perform an exact multiplication to know if the answer you are getting is sensible. To do this, students need to know the effect of multiplying multi-digit numbers. Students need to be able to take into account the magnitude of each of the two numbers being multiplied.
For example:
| 10 x 4 = 40 | 10 x 40 = 400 | 30 x 4 = 120 | 30 x 40 = 1200 |
| 100 x 4 = 400 | 100 x 40 = 4000 |
300 x 4 = 1200 |
300 x 40 = 12 000 |
NOTE:
Beware of rules of thumb like "count up the zeros" which work most of the time but does not show why it works. For example 50 x 40 could easily be wrongly written as 200 (2 followed by two zeros) instead of 2000 (20 followed by two zeros). The Numeracy Professional Development Book 6, Teaching Multiplication and Division, has sections which deal with this, for example "Multiplying tens".
Does not use compensation
These students can be challenged to see if compensation is possible and to explore it further.
- Firstly ask the student(s) "Is your answer too big, too small, or about right?" and "Why did you say that?" This will reveal more about their estimation skills.
- If they answer "Too small" or "Too big" ask them "About how much too small/big is it?" This emphasises that the compensation itself is an estimate, not an exact answer (unless they can perform the multiplication and additions/subtractions easily, preferably mentally). For front-end estimation, the answer is always too small. If just one number is rounded, the direction of compensation is easy to see.
Compensates "additively"
Student who do this sensibly (i.e. to tidy numbers, etc.) are still estimating. They are, however, bringing an element of additive thinking to a multiplicative situation. This will become particularly apparent if they are asked if their estimate is bigger than, smaller than, or close to the exact answer. Many will say that it is close because each number was adjusted by the same amount. If the student compensates additively to a question such as part c) they may respond "94 × 56 is close to 90 × 60 = 5400 because one number has gone up by 4 and one has come down by 4" they may be compensating without a full multiplicative approach. This is an additive approach, rather than multiplicative (or perhaps we could say additive rather than proportional) approach. Get a group of students who responded like this together and present them with this alternative strategies for estimating 94 × 56:
- Ask "What about 100 × 50 = 5000 as an estimate for 94 × 56? One number goes up by 6 and one goes down by 6. Does this mean that the exact answer is very close to 5000?" This presents the students with a cognitive conflict, because they will think that 5400 and 5000 are both very close to the correct answer. Get them to try and resolve this paradox. They may use diagrams, exact computations etc, but they must come up with an explanation. Actually 5000 under-estimates and 5400 over-estimates the exact answer. The clue is that one number must increase proportionately as much as the other one decreases for the answer to be close to the exact answer. So if 94 goes up to 100, that is about a 6% increase, so 56 should drop by about 6%, i.e. about 3, i.e. 100 × 53 = 5300 is close! Alternatively they could say that 94 is about twice 56 so if 94 goes up by 6 to 100, 56 should come down by about half of 6, i.e. 3. This is Stage 8 on the Number Framework - Advanced proportional part-whole thinking, and is rarely seen with Year 8 students.




