Fraction shapes

Fraction shapes

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about dividing a range of shapes into a given fraction.
 
Draw lines to help you shade the fraction for each shape below.
a)

\(1 \over 4\) of the circle.
  
b) \(1 \over 5\) of the pentagon.
 
c) Shade \(1 \over 7\) of the rectangle.
 
d) Shade \(1 \over 3\)of the square.

 

Task administration: 
This task can be completed with pencil and paper.
Level:
2
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Keywords: 
fractions, part-whole fractions, partitioning
Description of task: 
Students draw lines to divide up shapes into fractional parts.
Answers/responses: 
  Y4 (11/2005)
a) 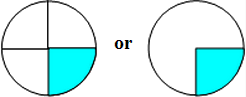moderate
b) 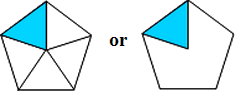difficult
c) difficult
d) 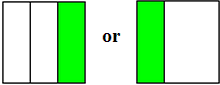very difficult
Based on a representative sample of 183 Y4 students in November 2005.
Teaching and learning: 
This resource is about showing how to find a range of given fractions for a variety of shapes.
Diagnostic and formative information: 
  Common error Likely misconception
a) - d) Divides shape into uneven sized pieces. The size of each piece doesn't matter – so long as the number of pieces is correct.
a) - d) Incorrect fraction of shape shaded Doesn't know how to show a fraction as a proportion of an area. (About a quarter of students unsuccessfully attempted to shade the given fraction without partitioning).
a) - d) Divides shape into even sized pieces/ no shading. Can use the bottom number (denominator) to divide the shape into parts, but doesn't show that they understand that each part is a unit fraction of the whole.
a) - d) One more partition than required. Either students are showing the ratio,(shaded over unshaded), or they are counting the lines as they draw them in the shape and the last line creates two parts.
Next steps: 
Students who did not show how they got the answer or shade the correct fraction of the shape may not know fractional notation, or have no understanding of the fraction as a part of a whole shape.

  1. Begin with a variety of simple shapes (square and rectangle) and try a progression of simple fractions "what is 1/2 ?, 1/4 ?", etc.
  2. Get students to recognise the relationship between the bottom number (denominator) and the number of equal-sized pieces the shape is partitioned into.
  3. Get students to partition a range of shapes into a range of fractions (with odd and even denominators).

NOTE:  Remind students they are finding a part of a whole, by asking:
"what is this part?" and
"what is the whole?"
Students who partition the shapes unevenly may not be aware that each fraction of the whole must be the same size – Asking the question "if it was pizza and you were hungry which of these fractions (same fractions) would you like?" and then discussing the concepts of fair share and evenness with simpler shapes, cutting them out and overlapping to check that they are equal sized.

Students who partition one more piece than required to show the fraction, could justify how many pieces they dividing the shape into.  Ask what fraction each piece will be, e.g., for the rectangle "if there are 8 pieces (all even) what fraction of the whole shape is that?" and "what fraction were we trying to find?".

For students who shade the correct part of the shape – encourage them to show how they know the shaded area is the given fraction of the whole shape.  This will confirm that they can partition the shape to find the part, rather than remember or approximate the fractional part of the whole.

NOTES:

  • Partitioning is an important concept leading into part-whole understanding of fractions.  It is important to use a variety of shapes and fractions to ensure that students are thinking, not simply remembering images or procedures to solve problems.
  • It is important for students to have a range of experiences with different representations of fractions to develop better understanding of what a fraction is.