Folding rectangles, squares and circles

Folding rectangles, squares and circles

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about folding shapes to show fractions.
 
 
a)
 i)

ii)

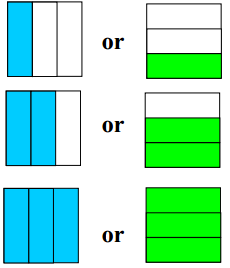
 Fold the rectangle to show halves. Show someone and tell them how you know it's halves.

Draw and shade what one-quarter of the rectangle looks like.
  

 

 
 
b)		  
i)		  
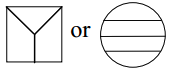
Fold the square to show thirds. Show someone and tell them how you know it's thirds.
  

 ii)  Draw and shade 1-third of the square.  iii)  Draw and shade 2-thirds of the square.  iv)  Draw and shade 3-thirds of the square.
 
 
 
 
 
 
 
 
 
 
 
  

 
 
c)		  
i)		  
Fold the circle to show quarters. Show someone and tell them how you know it's quarters.
  

 ii) Draw and shade 1-quarter of the circle.  iii) Draw and shade 3-quarters of the circle.  iv) Draw and shade 5-quarters of the circle.

 
 
 
 
 
 
 
 		  

 

 
Task administration: 

This task is completed with pencil, colouring pencils or felt pens, and paper.

Equipment:

pre cut paper shapes (circles, squares, rectangles) 1-2 of each shape for each student.

  • This resource is designed to be used with a small group of students.
  • Students can also share their partitions with peers or small groups.
  • Once students have shown their partitions (to the teacher, peer or group), they could continue on to the other questions.
Levels:
2, 3
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Keywords: 
fractions, partitioning, part-whole fractions, improper fractions, peer assessment, practical
Description of task: 
Students fold pieces of paper shaped as a rectangle, square, and circle to show fractions.
Curriculum Links: 
This resource can be used to help to identify students' understanding of partitioning to find fractions.
A possible progression for understanding could involve partitioning and drawing:
  • half and quarter of simple 2-dimensional shapes
  • unit fractions of 2-dimensional shapes
  • simple fractions of 2-dimensional shapes
  • simple and improper fractions of 2-dimensional shapes.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Multiplicative thinking, sets 3-4
Multiplicative thinking, sets 4-5
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
a)

 

 i) 
ii)		 Rectangle folded in half (2 equal-sized parts)
b)

 
i)
ii)

 

 Square folded in thirds (3 equal-sized parts)*
c)

 
i)
ii)
 
 
 
 
  
iii)
 
 
 
 
iv)

 

 Circle folded in quarters (4 equal-sized parts)*

NOTE: If students show  ask them how they know that the parts are equal.

Teaching and learning: 
This resource explores folding different shapes to represent fractions. In order for students to develop a more robust part-whole understanding of fraction, they need to be able to partition a wide range of shapes and sets into many different parts, and name the parts - including improper fractions. Click on the link for further information about partitioning and how it supports fractional understanding.

 

Diagnostic and formative information: 

The three major misconceptions for this assessment task are:

  1. not folding into the correct number of parts(partitioning);
  2. not ensuring that the parts are equal-sized (partitioning); and
  3. not being able to work out how to represent a whole or an improper fraction.
Next steps: 

Partitioning misconceptions
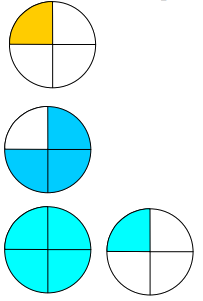
For students who tried to fold (or draw) the shapes  ask them how they know that the parts are equal, 

and if there is another way to partition that can be more easily checked.

For students who had difficulty partitioning the shapes into the correct number of or equal-sized parts: (1) Ask them when a shape is made into halves/thirds/quarters how many parts of the shape there are; and (2) What they notice about the parts - if they were food and being shared out would the parts be fair? Give students the opportunity to use folding or cutting to divide up shapes and encourage them to explain how they know the partitions are even, and how they could justify this to somebody else.

Students could also be asked to partition the shapes in different ways. It is important that students further develop their experiences of partitioning, starting with:

  • halving of basic shapes, then halving multiple times to derive other parts;
  • partitioning a variety of shapes: squares, two squares, rectangles, circles, hexagons (which may be easier to partition for younger students), etc.;
  • partitioning shapes into a different number of pieces (e.g., 3, 5, 6, 7, 9, etc).

By partitioning shapes into an odd number of parts and by using a number of shapes, students can develop a more robust understanding of partitioning. This variety ensures that they are not just memorising how to partition certain shapes, but that they have the ability to partition any simple shape and understand the importance of these parts being equal-sized.

Whole fractions and improper fractions
For students who had difficulty representing 3/3 or 5/4 in the assessment task, encourage them to recognise that building up to these fractions is comparable to counting with the fraction as a unit, e.g., comparing 1/4, 2/4, 3/4, 4/4, 5/4 to one lot of 1/4, i.e., 1 x 1/4, two lots of 1/4, i.e., 2 x 1/4, three lots of 1/4, i.e., 3 x 1/4, etc. For improper fractions five lots of 1/4 is 5 x 1/4, and is greater than a whole shape. Once they have the same unit (i.e., fractions with the same denominator), the numerators can be added. Conversely, if they are different units, they cannot be added directly (e.g., 1/4 and 1/5).

Read more about about partitioning and how it supports fractional understanding.