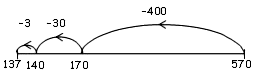Number line subtraction II

Number line subtraction II

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about showing how to solve subtraction equations on a number line.
For the questions below show how to solve the equations on the number line. 

Read through the example in the box before you start.

Example: Sarah had to solve this problem: 96 –    =  64.
She knew that 96 – 30 = 66, and that 66 – 2 = 64. 
So she showed this on the number line and then wrote the answer in the box:
 
a)

 
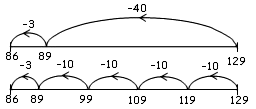
Use the number line below to show how to solve the equation:  129 –    = 86
 
 
 
 
89-129-number-line.png
 
b)

 

Use the number line below to show how to solve the equation:  570 –    = 137 
 
 
 
 
137-570-number-line.png
 
c)

 
Use the number line below to show how to solve the equation:  786 –    = 428
 
 
 
 
428-786-number-line.png
 
d)

 
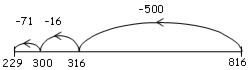
Use the number line below to show how to solve the equation:  816 –    = 229
 
 
 
 
 
229-816-number-line.png
Task administration: 
This task is completed with pencil and paper only.
Level:
3
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Keywords: 
number lines, subtraction
Description of task: 
Students use a number line to show how to solve whole number subtraction problems.
Curriculum Links: 
This resource can help to identify students' ability to apply additive and simple multiplicative ideas flexibly to combine or partition whole numbers to solve subtraction problems.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Additive thinking, sets 6-7
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
  Y6 (06/2006)
a)

 

43
The number line is used to show jumps added/subtracted that use the sequential nature of the number line, e.g.,

or other acceptable jumps that show the equation.

 moderate
moderate
b)

 

433
The number line is used to show jumps added/subtracted that use the sequential nature of the number line, e.g.,

or other acceptable jumps that show the equation.

 difficult
difficult
c)

 

358
The number line is used to show jumps added/subtracted that use the sequential nature of the number line, e.g.,

or other acceptable jumps that show the equation.

 very difficult
difficult
d)

 

587
The number line is used to show jumps added/subtracted that use the sequential nature of the number line, e.g.,

or other acceptable jumps that show the equation.

 very difficult
very difficult
Based on a representative sample of 152 students
 
NOTE:

  1. Accept even if arrows are missing, as long as the intent is clear.
  2. Subtraction equations can also be represented as addition jumps on the number line (known as complementary addition).
Teaching and learning: 
This assessment resource is about whether students can show the process of solving a subtraction equation on a number line and what strategies they use to do so.  Students who have not used a number line to solve problems will need to learn how to show addition and subtraction jumps on a number line.
Next steps: 
Some students solve the problems using another method and attempt to represent the solution on the number line rather than showing how the solution can be reached on the number line.  In this case the lines drawn on the number line do not necessarily represent additions or subtractions.  Students may write the answer on the number line and try to draw appropriate visual lines.  For example, 86 +  43 = 129 and the number line drawn is …

Without the size of the jumps indicated there is no evidence that the number line is actually being used to solve or even represent the equation (although they have solved the equation using some other strategy).

As the resource is about representing operations on a number line, students who responded like this may need introductory work looking at how addition and subtraction can be shown as jumps on a number line.  Get students to use a basic addition problems [resource: Number line addition (L2) or  (L3)]. With the examples, ask questions like "What happens if I start here and add 10?", or "How do we show the addition on the number line?". Encourage students to represent – not count out and draw in marks, but just draw – an approximate jump, mark the size and direction of the jump, and the new location on the number line.

For students who can show basic place value jumps on the number line, encourage them to use fewer jumps to solve the equation more efficiently and reflect on which strategies best suit the particular equation.  This may involve using tidy numbers or compatible numbers rather than jumps made strictly by place value partitioning, and may also involve jumping past the target number, then back to it.

For students who solved the equation using the vertical algorithm and then represented the answer on the number line, encourage them to use jumps on the number line as a tool to solve and reflect on the jumps that could make this most efficient (as above).

Links to the Numeracy project
Showing how to solve addition problems on a number line can require jumping to tidy numbers, or using tidy numbers to make the jumps, and then making an adjustment to complete the equation.  Students can also use elements from place value partitioning, or compatible numbers, to jump along the number line.

A simple place value partitioning strategy with unitised jumps (i.e., jumps of 10 + 10 + 10 + 10 instead of + 40) may indicate an early additive part-whole understanding.  To indicate advanced additive part-whole thinking, students would use fewer jumps (more efficient jumps) to solve equations and be able to use or identify different ways to show how to solve the equation (multiple strategies).
 
Figure it out:
  • Maths Detective (Number sense and Algebraic thinking, L3, book 2, pages 2-4), and
  • Tidying up (Number sense and Algebraic thinking, L3, book 1, pages 2-4).
Numeracy:
Using tidy numbers: refer to Jumping the number line, Problems like 23 +  ?  = 71, and for using place-value partitioning: refer to Problems like 37 + ?   = 79  (both Book 5: Teaching addition, subtraction and place value, pages 33-36).