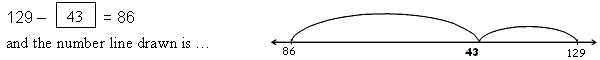Number line subtraction

Number line subtraction

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about showing how to solve equations on a number line.
Read through the example in the box before you start.
 
Example:
Pere had to solve 46 – = 24 using a number line.
He knew that 46 – 20 = 26, and that 26 – 2 = 24, so 46 – 22 = 24
He showed this as jumps on the number line and then wrote the answer in the box:

For each question below:

  1. Show how to solve the equations on the number line.
  2. Write the answer in the empty box.
 
a)
 
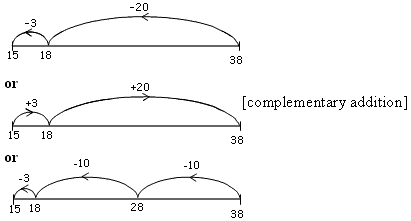
Use the number line below to show how to solve:  38 –  = 15
 
 
 
 
 
numberline-15-38.png
 
 
b)
 
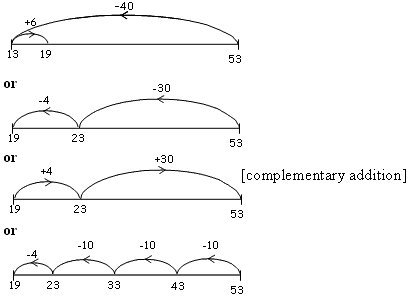
Use the number line below to show how to solve:  53 –  = 19
 
 
 
 
 
numberline-19-53.png
 
 
c)
 
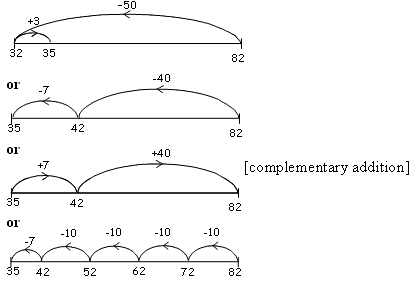
Use the number line below to show how to solve:  82 –  = 35
 
 
 
 
 
numberline-35-82.png
Task administration: 
This task is completed with pencil and paper only.
Level:
2
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Keywords: 
number lines, subtraction
Description of task: 
Students use a number line to show how to solve whole number subtraction problems.
Curriculum Links: 
This resource can help to identify students' ability to use basic facts and knowledge of place value and partitioning whole numbers to solve subtraction problems.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Additive thinking, set 5
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
  Y4 (11/2006)
a)

23
The number line is used to show jumps added/subtracted that use the sequential nature of the number line, e.g.,

or other acceptable jumps that show the equation.

difficult
moderate
b) 34
The number line is used to show jumps added/subtracted that use the sequential nature of the number line, e.g.,

or other acceptable jumps that show the equation.		 difficult
difficult
c) 47
The number line is used to show jumps added/subtracted that use the sequential nature of the number line, e.g.,

or other acceptable jumps that show the equation.		 very difficult
difficult
 
Based on a representative sample of 149 students.

NOTE:

  1. Accept even if arrows are missing, as long as the intent is clear.
  2. Subtraction equations can also be represented as addition jumps on the number line (known as complementary addition).
Teaching and learning: 
This assessment resource is about whether students can show the process of solving a subtraction equation on a number line and what strategies they use to do so.  Students who have not used a number line to solve problems will need to learn how to show addition and subtraction jumps on a number line.
 
Links to the Numeracy project

Showing how to solve addition problems on a number line can require jumping to tidy numbers, or using tidy numbers to make the jumps, and then making an adjustment to complete the equation.  Students can also use elements from place value partitioning, or compatible numbers, to jump along the number line.
A simple place value partitioning strategy with unitised jumps (i.e., jumps of 10 + 10 + 10 + 10 instead of + 40) may indicate an early additive part-whole understanding.  To indicate advanced additive part-whole thinking, students would use fewer jumps (more efficient jumps) to solve equations and be able to use or identify different ways to show how to solve the equation (multiple strategies).
Diagnostic and formative information: 
About a third of students did not attempt to show the jumps on the number line.  This may have been due to them not being able to use a number line to show the operation (addition/subtraction).
Next steps: 
Rather than using the number line to solve the subtraction problem, some students solved the problem first using some other method and tried to draw appropriate lines on the number line to represent the solution.
For example,


As the resource is about representing operations on a number line, students who responded like this may need introductory work looking at how addition and subtraction can be shown as jumps on a number line. Get students to use basic addition problems such as Number line addition.  With the examples, ask questions like "What happens if I start here and add 10?", or "How do we show the addition on the number line?" Encourage students to represent – not count out and draw in marks, but just draw an approximate jump, mark the size and direction of the jump, and the new location on the number line.

For students who can show basic place value jumps on the number line (i.e., –10, –10, –10, etc), encourage them to use fewer jumps to solve the equation more efficiently and reflect on which strategies best suit each particular equation.  This may involve using tidy numbers or compatible numbers rather than jumps made strictly by place value partitioning, and may also involve jumping past the target number, then back to it.

For students who solved the equation using the vertical algorithm and then represented the answer on the number line, encourage them to use jumps on the number line as a tool to solve, and reflect on the jumps that could make this most efficient (as above).

Figure it out:
Maths Detective (Number sense and Algebraic thinking, L3, book 2, pages 2-4), and 
Tidying up (Number sense and Algebraic thinking, L3, book 1, pages 2-4).

Numeracy Development: 

Using tidy numbers: refer to Jumping the number line, Problems like 23 + □ = 71,and for using place-value partitioning: refer to Problems like 37 + □ = 79  (both Book 5: Teaching addition, subtraction and place value, pages 33-36).