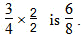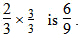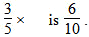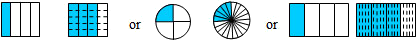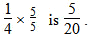Same sized fractions

This task is about how different fraction numbers can be the same size.

Sometimes drawing fractions can help show how different looking fractions can be the same size.

a) Draw or explain how the fraction \(3 \over 4\) is the same as \(6 \over 8\).

b) Draw or explain how the fraction \(2 \over 3\) is the same as \(6 \over 9\).

c) Draw or explain how the fraction \(3 \over 5\) is the same as \(6 \over 10\).

d) Draw or explain how the fraction \(1 \over 4\) is the same as \(5 \over 20\).

Answers/responses:

		Y6 (06/2009)
a)	Student explanation involves any 1 of: Accurate diagram of both fractions that can be compared (i.e., both representations have the same whole unit) showing how they are the same size, e.g., Discussion about the relationship between the top and bottom numbers being the same (e.g., talks about the fractional relationship – 3 is ³/₄ of 4, and 6 is ³/₄ of 8) Indicating they are the same because the top and bottom components are both multiplied by 2, and ²/₂ = 1 (multiplying by 1 leaves it the same) e.g.,	moderate
b)	Student explanation involves any 1 of: Accurate diagram of both fractions that can be compared (i.e., both representations have the same whole unit) showing how they are the same size, e.g., Discussion about the relationship between the top and bottom numbers being the same (e.g., talks about the fractional relationship – 2 is ¹/₃ of 6, and 3 is ¹/₃ of 9) Indicating they are the same because the top and bottom components are both multiplied by 3, and ³/₃ = 1 (multiplying by 1 leaves it the same) e.g.,	difficult
c)	Student explanation involves any 1 of: Accurate diagram of both fractions that can be compared (i.e., both representations have the same whole unit) showing how they are the same size, e.g., Discussion about the relationship between the top and bottom numbers being the same (e.g., talks about the fractional relationship, 2 is ¹/₃ of 6, and 3 is ¹/₃ of 9); Indicating they are the same because the top and bottom components are both multiplied by 2, and ²/₂ = 1 (multiplying by 1 leaves it the same) e.g.,	difficult
d)	Student explanation involves any 1 of: Accurate diagram of both fractions that can be compared (i.e., both representations have the same whole unit) showing how they are the same size, e.g., Discussion about the relationship between the top and bottom numbers being the same (e.g., talks about the fractional relationship – 1 is ¹/₄ of 4, and 5 is ¹/₄ of 20, or 1 goes into 4 four times and 5 goes into 20 four times) Indicating they are the same because the top and bottom components are both multiplied by 5, and ⁵/₅ = 1 (multiplying by 1 leaves it the same) e.g.,	difficult

Based on a representative sample of 189 students.

NOTE:

For all questions accept other accurate and comparable strategies.
For diagrams, a certain degree of accuracy was required to indicate that the argument was conceptually correct. This meant both the number of partitions was correct and that the parts were fairly evenly partitioned.

Teaching and learning:

There are several strategies that can be used to compare fractions: students can draw representations of both fractions and draw lines to show how they are of equivalent size. Underlying this is the understanding that a shape or group of objects that represent a fraction can be partitioned (subdivided) in different ways, and when the partitions of two shapes or groups are the same and the area or number of objects are the same then the fraction (of the whole) is the same.

Prior Knowledge
An understanding that fraction notation represents a number of equal-sized parts.
The ability to draw a diagram to represent a fraction, and that comparing fractions should involve the same whole (same-sized shape, same number of counters, etc.) for both fractions being compared.

Diagnostic and formative information:

Students used a range of strategies to show or describe how the two fractions were the same. Over a third of students drew diagrams of comparable fractions. A small number of students (under 10%) reasoned the equivalence by discussing how the proportions of the top to bottom number were the same.

	Common error	Likely misconception
a)- d)		Cannot draw part-whole representation of fractions Students can draw a partitioned shape, but do not connect up that it is the shading of the drawing (whole unit) that represents the fraction.
a)- d)		Partitioning error (unequal size of parts or incorrect number of parts) Students do not partition shapes into equal-sized parts (for this comparison) or do not create the correct number of parts to represent the fraction.
a)		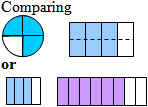Comparing different shapes Students draw two pictures that are not comparable (i.e., they don't share a common whole to be compared). Students are not connecting up that comparing two fractions involves an assumption that they share a common whole (or a fraction of a common unit).
a)		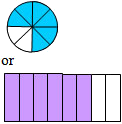Drawing only one shape (incomplete) Students drew one of the shapes, but without any indication or labelling. This was regarded as an incomplete argument. An example of a possible statement for the circle shape "this fraction shows 6 eighths, but it also represents 3 quarters". For the rectangle shape some indication of the 3 quarters (i.e., how it is 3 quarters) would be required, such as vertical lines to indicate the quarter-ness of the shape.
a) b) c) d)	Double ³/₄ to get ⁶/₈ ²/₃ times 3 to get ⁶/₉ Double ³/₅ to get ⁶/₁₀ ¹/₄ times 5 to get ⁵/₂₀	Insufficient argument (suggesting fractions are not equivalent) Although this is the start of an argument it is insufficient to explain or show how the fractions are the same – it may even suggest that one fraction is twice as large as another and therefore not equivalent. This argument may also have been written "they are the same because ⁶/₈ is half of ³/₄ " or " ³/₄ + ³/₄ = ⁶/₈ " further indicating another misconception about the larger number being smaller pieces.

Next steps:

Cannot draw accurate part-whole representation of fractions
Students who did not draw an accurate diagram to represent a fraction (partitioning error or drawing error) may benefit from first exploring partitioning exercises, then drawing fraction diagrams (Shaded fractions and Fraction shapes) without the need to compare to other fractions. Get students to partition shapes (also sets and amounts) into parts and justify their answers by explaining, showing (with equipment), or drawing. They should recognise that one piece is a unit fraction of the whole. Encourage students to think about how they could construct each fraction (e.g., partition then build up) and then find common ground on which to compare them. The idea of equal sized parts and the correct number of partitions is an important piece of knowledge to support part-whole representations of fractions before attempting to explain ideas about equivalence.

Comparing a different whole
Students who drew different types (or sizes) of shapes could be asked how the diagrams show the fractions are the same. When comparing fractions it may help to have students consider it in this way:

Use two rectangle shapes the same size;
Partition each into the number required;
Lay these next to each other and discuss how much of the rectangle they each are.

For example, comparing ³/₅ and ⁶/₁₀

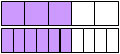
Rectangles allow for easy construction and easy comparison.
The idea of comparing and equivalence is based around relative thinking, and could be explored by looking at two diagrams with a different whole that challenge a simple known fact (e.g., ¹/₃ > ¹/₄ ) ¹/₃ and ¹/₄ and asking "how come this diagram doesn't show ¹/₃ > ¹/₄ ?

Drawing only one shape (second shape)
Implicit in this may be that, because they are fractions of the same whole, the fractions can both be shown on one shape (this is true if it is supported with an explanation). Students who drew a diagram of only the second shape (with more partitions) may benefit from explaining their diagram to a peer and then writing their explanation alongside their diagram.

Drawing only one shape (first shape)
This misconception suggests that students may not have much experience creating fraction representations beyond the common basic fractions, and require opportunity to partition and build up other fractions using different shapes (Sharing shapes), as well as identify fractions from other diagrams (Shaded fractions and Fraction shapes). Students who drew only the first shape could be asked how they think the second shape could be drawn. They could explore easier shapes to partition and shade (such as rectangles). Some discussion may also be needed about comparing fractions with the same whole (see Comparing a different whole, above).

Students who answered with an insufficient explanation
Students could also be asked what they mean when they say "double" and compare this doubling to a whole number (which doubles the size). Students may also need to have a "sufficient" explanation modelled and made explicit to them. Click on the link to the English resource for further information about writing an explanation.

Correct multiplicative explanation
For students who multiplied the denominator and numerator by the required factor to show (mathematically) that they are the same may be showing a learned method and may not know why the method works (i.e., it is multiplying by the different forms of 1, ²/₂ , ³/₃ , ⁵/₅ , etc). This method may also obscure or interfere with students developing an understanding about fractions and equivalence. If students show this method, they could also be asked how this means that the fractions are equivalent and why they multiplied top and bottom by that number. They could also be asked to explain another way – using diagrams to show their reasoning.

Correct diagrammatic explanations
For students who drew sufficient diagrams encourage them to find a way to explain equivalence using the denominator and the numerator. This can be supported by exploring patterns and relationships of equivalent fractions i.e., other names for the same fractions: ²/₃ is also ⁴/₆ , ⁸/₁₂ , ¹⁰/₁₅ , etc.

You are here

Resource user links

Same sized fractions

Same sized fractions