Taxi charges

Taxi charges

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about reading information from a graph.
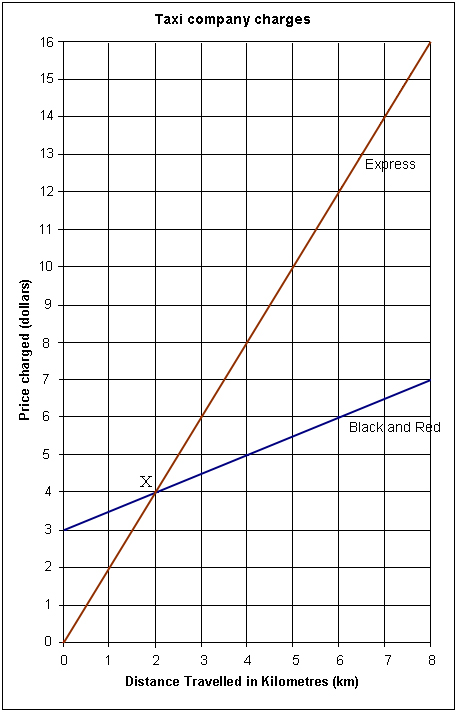
graph of two taxi company charges
 
On Friday nights Shane catches a taxi home. The graph shows the prices charged by two different taxi companies - Black and Red Taxis and Express Taxis.
Use the graph to answer the questions that follow.
 
a)
If Shane had only $6.00, how far could be travelled if Black and Red Taxis were used? __________ km
 
b)
Which taxi company would be cheaper, and by how much, if Shane was travelling 8 kilometres?
 
____________________________ would be cheaper by $ _______________________
 
c) Point X on the graph is where the 2 lines cross. What does point X represent?
 

 
 
d)
Let C = "price charged" and k = "number of kilometres".
Complete an equation to show what each taxi company charges.
 
  i)   Express Taxis: C = ____________________
 
ii)  Black and Red Taxis: C = ____________________
Task administration: 
This task is completed with pencil and paper only.
Level:
5
Curriculum info: 
Maths, Number and Algebra, Equations and expressions
Keywords: 
graph interpretation, linear equations, breakeven points
Description of task: 
Students interpret a graph of taxi company charges to show which company is cheaper and complete a rule for each company's charges. They also identify the distance at which each company charges the same amount.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Using symbols and expressions to think mathematically, sets 6-7
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
 

Y10 (08/2001)
a)   6 very easy
b)   Black and Red, 9 easy
c)   The distance for which both companies charge the same price. moderate
d) i)
ii)		 2k
3 + 0.5k		 moderate
difficult
Diagnostic and formative information: 
 

Common error

Likely reason

a)

3

 Reading off 'Express' Taxi's graph line.

b)

Black and Red by $10.

 Incorrect counting of grid squares.

c)

Where they both charge the same price.

 Fails to mention that at this price they travel the same distance.

d) i)

16 + 8k
16k = 8

In the expression uses last points on the x and y axis.