What's the whole unit?

What's the whole unit?

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about fractions of different whole units.
  
Key   
   = 1 full cola bottle =  one 8-pack  = 1 case
   = 1 empty cola bottle
   = one 4-pack

Use the diagram of the two cases below to answer the questions that follow.

The first question has been done for you.

a)
 
How many 4-packs of full cola bottles are there? 6 1/2
(include any fractional part of a 4-pack)
 
  
b)

How many 8-packs of full cola bottles are there? _____
(include any fractional part of an 8-pack)

 
c)

How many cases of full cola bottles are there? _____
(include any fractional part of a case)

 
d)
What fraction of all the bottles are full? _____
 
Task administration: 
This task is completed with pencil and paper only.
Level:
5
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Keywords: 
fractions, part-whole fractions, unitising, key competencies
Description of task: 
Students answer questions about fractions of different wholes (units).
Curriculum Links: 
Key competencies
This resource involves understanding complex relationships within fractional/proportional thinking and recording their reasoning. This relates to the Key Competencies: Thinking and Using language, symbols and text.
Answers/responses: 
    Y10 (10/2009)
a) 6 1/2 or equivalent. given
b) 3 1/4 or equivalent. very easy
c) 1 5/8 or equivalent. easy
d) 26/32 or 13/16 or equivalent. easy

 

Teaching and learning: 

This resource explores the concept of unitising with quantities using fractions. Unitising can be defined as the assignment of a unit of measure to a quantity or "chunk" that make up a given quantity (Lamon, 2007). Unitising involves understanding of partitioning and equivalence to develop flexible thinking about fraction situations. This flexibility can in turn support further understanding about equivalence and fractions as rational numbers (in particular quotients – the result of division).
See Fractional thinking concept map: Unitising with fractions.

In this resource unitising involves finding a number of different units of measurement for a given quantity. The chunks (units) are all getting larger (e.g., chunks of 4-packs, 8-packs, cases, whole quantity), and the fractions that describe them are getting smaller. As an extension to this resource, students can also create own different chunks to describe the proportion of full bottles (e.g., using 2-packs, 3-packs, etc instead of 4-packs and 8-packs).

Diagnostic and formative information: 
  Common error Likely misconception
    Students can count the full units, but not correctly identify the fractional part of the answer
b)

3 1/2

 Students counted the 8-packs, but kept the 1/2 (4-pack) instead of recognising that 1/2 a 4-pack would be 1/4 of an 8-pack.
c) 1 1/2 Students counted the 8-packs, but kept the 1/2 (4-pack) instead of recognising that 1/2 a 4-pack would be 1/4 of an 8-pack. 

Examples of students' explanations (sufficient)

These could be used for discussion involving moderation of students' strategies.

  • The questions divide the overall amount of full bottles into sections, e.g., a full case is 16 but halved is an 8-pack, etc. The overall amount stays the same.
  • The bigger the pack of bottles are the smaller the fractions; because you can't fit as many packs, e.g., 4-packs go 6 1/2 times, whereas 8-packs (which are bigger) go in 3 1/4 times.
  • The amount of full bottles in each group changes: from 4 to 8 to 16 (doubling each time). The fraction halves every time the number of full bottles in each group doubles.
  • 6 1/2 4-packs = 3 1/4 8-packs and 1 case contains 16 bottles. Two 4-packs = 1 8-pack; 2 8-packs = 1 case.
  • Because in every question the whole unit is different.
  • Because the way of measuring them is changing, e.g., 4-pack, 8-pack, case etc.
  • They are using different units, e.g., 1 bottle, 4 bottles, 8 bottles, 16 bottles.
  • Asking for the fractions for different amounts within the case.
  • Each question is using different types of units to see how many bottles are full.
  • Because the question is different: first it asks how many 4-packs, then 8-packs, but the number of bottles is still the same.
  • We are working out the number of full bottles in different sized packs/case.
  • The question asks for different units so the answers are different.

Examples of students' explanations (insufficient)

  • Asking the questions in different measurements.
  • The total you take away from is different and the answer that they want is different, e.g., mm is different to cm; 1/2 is different to 1/3.
  • Because you are referring to different fractions' size.
  • Each symbol has a different amount of coke bottles in it.
  • Asking about packs not bottles.
  • The sizes are bigger so 4 4-packs = 1 case which means more coke in the numbers.
  • They are asking different questions but using the same thing, .e.g., full bottles.
  • The answer isn't simplified.
Note : Those who gave the fraction answer in its simplest form had higher mean ability than those who gave a correct answer unsimplified.
Next steps: 

Can count the full units, but does not correctly identify the fractional part of the answer
It is likely that students understand the idea that the bottles can be described as different units, but are limited in their ability to work with fractions (especially those who wrote 31/2 for question b), and 11/2 or 13/4 for question c). Get them to circle the units across both cases for each question and then describe their answer referring to the whole number part and the fractional part on the diagram, e.g., for 4-packs, circle all the 4-packs, then the fractional part becomes more obviously half a 4-pack.

or for 8-packs
(31/4)

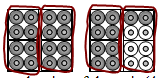Then encourage students to explore the relationship between the size of the unit (4, 8, case, etc.) and the fractional value that describes how many units there are. Ask what happens to the fraction when we double the size of the unit. What about halving? Ask students to predict how many 2-packs, e.g., If there are 61/2 4-packs, how many 2-packs are there?

Insufficient explanation
For students who gave an insufficient explanation about why the answers (fractions) changed while the number of bottles stayed the same, ask them what whole the fractions were of (e.g., 31/4 of what? bottles, packs or cases?). Get students to relate the unit of measurement with the fraction answer. Putting the results in a table to help them see how the numbers change (use the diagram of the cases and work with the non simplified fractions and then simplify afterwards–mark the units of measurement if required), e.g.,

Number of bottles in pack Fraction answer
4 6 2/4
8 3 2/8
16 1 10/16
32 26/32

Sufficient explanation, but missing the recognition of the relationship between the unit and the fraction answer.
For students who gave a sufficient explanation about why the fraction answers changed while the number of bottles stayed the same, but did not talk about the relationship between fractional value and the size of the unit, teachers could:

  1. Ask students what is happening to the unit in each question (answer: doubling).
  2. Then ask students what is happening to the fractional amount of those units of measurement.
  3. See if they can connect the halving and doubling and therefore the multiplicative relationship between the fractional value and the units. Students could then be asked, If the unit was a 16-pack what would the fraction be? or If the unit was a 12-pack what would the fraction be? (harder because it is no longer doubling).

Writing simplest form
All students should be encouraged to write their fraction answers in its simplest form to further indicate their understanding of the part-whole nature of fraction numbers and the multiplicative relationships between the numerator and the denominator.
Note: Writing the answers in simplest form can mask the halving and doubling relationship of this item.

For more information about unitising with fractions, see Fractional thinking concept map: Unitising with fractions.
 
Lamon, S. J. (2007). Teaching fractions and ratios for understanding: Essential content knowledge and instructional strategies for teachers. New Jersey : Lawrence Erlbaum.