Parts, wholes and other parts
| a) |
|
| b) |
What fraction is
|
| c) |
What fraction is
|
| d) |
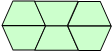 is 64 of a whole shape. Draw what the whole shape would look like. is 64 of a whole shape. Draw what the whole shape would look like.
|
| e) |
What fraction is
|
This resource explores students' ability to think about part-whole fraction problems differently. Instead of being shown a whole shape with a shaded part and asked what fraction is shaded, students are given a shape and told what fractional value it represents. They are then asked to find another fractional part or the whole (referent whole). This requires them to use the information given to think dynamically about the relationships between the part and the whole rather than simply naming a shaded part from a given whole. This way of asking part-whole fraction questions challenges a learned "process" for solving such questions, and requires flexible thinking to make sense of the information given as the referent whole changes for each question. Key competencies: Thinking.
| Y8 (11/2009) | ||
| a) | 1/8 | easy |
| b) | 11/3 or 4/3 * | moderate |
| c) | 7/12 | difficult |
| d) |
 or similar shape. or similar shape. |
difficult |
| e) | 32/3 or 11/3 * | moderate |
*NOTE: Students who wrote their answers to questions b) and e) as mixed fraction had a notably higher mean ability than students who gave their answers as improper fractions. Both answers are correct. However as an extension students who wrote their answer as improper fractions could be asked to write their answer as a mixed fraction or show it on a number line (e.g., show 11/3 on a number line).
Key Competencies: Thinking
This resource explores students' ability to think about part-whole fraction problems differently. Instead of being shown a whole shape with a shaded part and asked what fraction is shaded, students are given a shape and told what fractional value it represents. They are then asked to find another fractional part or the whole (referent whole). This requires them to use the information given to think dynamically about the relationships between the part and the whole rather than simply naming a shaded part from a given whole. This way of asking part-whole fraction questions challenges a learned "process" for solving such questions, and requires flexible thinking to make sense of the information given as the referent whole changes for each question. Key competencies: Thinking.
| Common error | Likely misconception | |
|
a) b) c) e) |
1/2 1/4 2/7 6/11 or 11/6 |
Changing/ignoring the referent whole This error could be a description of the latter shape to the former (or vice versa). For example in question a)  is half of is half of  . Here . Here  is used as the referent whole. It could also relate to a reversion whole number concepts where the second shape is half of 1/4 which is mistakenly identified as 1/2 (because 2 is half of 4). For questions a) and b) about one-eighth of students indicated this misconception is used as the referent whole. It could also relate to a reversion whole number concepts where the second shape is half of 1/4 which is mistakenly identified as 1/2 (because 2 is half of 4). For questions a) and b) about one-eighth of students indicated this misconception |
|
c) e) |
1/7 1/11 |
Interpreting only the second diagram Students ignored the value of the first shape and used the second shape to work out what one piece represents, e.g., for  1 out of 7 = 1/7 ; or one piece of 1 out of 7 = 1/7 ; or one piece of  is 1/11 . is 1/11 . |
| c) | 7/6 or 11/6 |
Using the wrong unit Students worked out the number of parts (7) in  , but ignored that it is 2 pieces that make up 1/6 , and use one piece, , but ignored that it is 2 pieces that make up 1/6 , and use one piece,  as 1/6 . as 1/6 . |
| d) |
Difficulty with representations of improper fractions Students did not draw a diagram of the referent whole given 6/4 . This question involves two aspects that students need to use to correctly draw the diagram: 1. knowing how to work with improper fractions; 2. being able to identify the "whole" from a given fraction. Both the following errors indicate a lack of understanding about representing improper fractions and being able to find a related fraction. |
|
| d) |
 |
Increasing the shape by two pieces About one-sixth of students drew a larger shape by two more parts. This is likely due to them interpreting 6/4 as 4/6 and attempting to add a third more (2 pieces). |
| d) |
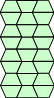 |
Making four lots of the shape to make a whole About one-seventh of students repeated a number of the 6/4 shapes to build up to some whole. |
This involves changing or not recognising what whole we are finding the fraction of. Students may have only explored fraction problems that find a part of a given whole. With this type of question in this resource students are given a part and required to either find the whole or another part.
Two ways to find another part are:
- Building up to the whole and then finding the new part of that whole, finding the whole–example or
- Recognising the relationship between the two different parts, finding parts example.
them (imaging). Asking students to explain what the whole shape is and what the part is may support them to clarify the part-whole idea of fraction. Encourage students to verbalise the strategies they use to work out the answer. Often students can identify and share more than one way of getting to an answer.
Using the wrong unit
Students who used the wrong unit in question c) may benefit from deconstructing their answer by asking what fraction one piece ( ) is, and then what fraction
) is, and then what fraction  represents.
represents.
Difficulty with representations of improper fractions
This misconception involves not recognising what the whole is in the question (Changing the referent whole misconception above), and difficulty representing improper fraction as diagrams.
It is likely that the problems students have representing improper fractions relate to the predominant use of fraction area diagrams that need make up to a whole rather than models such as number lines which can be used to represent all fractions as numbers. Students need to develop an understanding that fractions can be greater than 1. They may have seen improper fractions written, but getting students to work with or draw improper fraction representations begins to explore their understandings about how the part and the whole interact.
Using the linear nature of Cuisenaires and fractions can support students to visualise fractions greater than 1 and provide succinct parts and wholes to work with, e.g., If red is 1/2 dark green is three of them 3 halves (3/2). Students could then be asked "What is 1 whole?".
Whole class discussion
Many of the above next steps can be explored in whole class discussion where students share and critique their own and others' strategies to develop a fuller understanding.
Writing improper fractions
While still correct, students who wrote their answers to questions b) and e) as improper fractions could be asked to write their answer as a mixed fraction or show it on a number line (e.g., show 11/3 on a number line). This would indicate a better understanding about fractions as numbers.
For more information about part-whole fractions and unitising, see the Fractional Thinking Concept Map.
Book 7: Teaching Fractions, Decimals and Percentages, 2006 (Numeracy Project Books)
Birthday cakes (Early/Advanced additive) explores giving students a part and asking them to find the whole (extending this to explore improper representations may be important to avoid misunderstanding about the whole.
Trains (Early/Advanced additive) involves using Cuisenaire rods to build up fractions (including improper fractions).

