Calculator patterns
|
|
||
|
Talia was using a calculator to make number patterns. If you keep pressing the
Fill in the boxes with a number. Fill in the circles with an operation sign (+, ×, ÷, or –). An example has been done for you. |
||
|
||
|
a) |
Talia pressed |
|
|
b) |
Pattern: 70, 62, 54, 46, 38 …
Taila pressed |
|
|
c) |
Pattern: 45, 36, 27, 18, 9 …
Taila pressed |
|
|
d) |
Pattern: 80, 40, 20, 10, 5 …
Taila pressed |
|



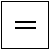 button
button








