Cover up II

Cover up II

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about showing how to find out how many counters are covered on an array.
 
For the questions below there are 10 × 10 (100) counters and some have been covered.
 
a) Show how to work out how many counters have been covered.
 
 
 
 
 

Answer: __________  

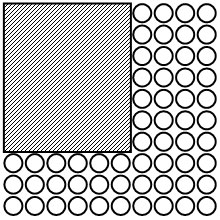
b) Show how to work out how many counters have been covered.

 
 
 
 
 

Answer: __________  

 
 
c) Show how to work out how many counters have been covered.
 
 
 
 
 

Answer: __________  

 
 

 

Task administration: 
This task is completed with pencil and paper only.
Level:
2
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Keywords: 
arrays, addition, multiplication, subtraction
Description of task: 
Students work out the number of covered counters on a 10 x 10 array.
Curriculum Links: 
This resource can help to identify students' ability to use basic facts and knowledge of place value and partitioning whole numbers to solve multiplication problems.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Additive thinking, set 5
Multiplicative thinking, sets 3-4
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
    Y4 (11/2006)
a) 60
working showing ...

  • multiplying columns and rows to solve – visible (100 – 4 × 10) or covered (6 × 10);
  • counting of the visible counters (and subtracting from 100);
  • group counting (either the covered or visible counters);
  • marking and counting the covered counters;
  • other correct working.

60 and sufficient working.

 easy
moderate

 

 

moderate
b) 42
working showing ...

  • multiplying columns and rows to solve – visible (100 – 6 × 3 + 10 × 4) or covered (6 × 7);
  • counting of the visible counters (and subtracting from 100);
  • group counting (either the covered or visible counters);
  • marking and counting the covered counters;
  • other correct working.

42 and sufficient working.

 difficult
difficult

 

 

very difficult
c) 64
working showing ...

  • multiplying columns and rows to solve – visible (100 – 4 × 9) or covered (8 × 8);
  • counting of the visible counters (and subtracting from 100)
    e.g., 100 – 10 – 10 – 8 – 8;
  • group counting (either the covered or visible counters);
  • marking and counting the covered counters;
  • other correct working.

64 and sufficient working.

 difficult
difficult

 

 

very difficult
Teaching and learning: 
This resource can help identify students that use counting, or part-whole (additive or multiplicative) strategies to solve imaging problems.
Diagnostic and formative information: 
  Common error Likely misconception
a)
b)
c)		 40
58
36		 Counts the visible counters but does not to subtract from 100 to find the solution.
c) 60 Counts the visible counters, but does not compensate for the four corners doubling up.
Next steps: 
For students who could not correctly count the number of counters covered, try asking:

  1. "How many counters are there altogether?" to check their understanding that there are 100 counters.
  2. "Is there a quicker way than counting to work out how many counters are visible/shown?".
    e.g., "How many across?" and "How many down?".
    Encourage a system rather than counting.
  3. "If we know how many there are in total and we know how many are shown, how could we find the number of counters that are covered?"

For students who correctly answered the number of covered counters, but didn't show how they worked it out, encourage them to verbalise their strategy to a partner then write it down and have the partner check it (and vice versa).
For students who marked in the covered counters, encourage them to find another way of solving the problem, e.g., counting the visible counters and subtracting them, counting groups (tens), then guide them to finding a non-counting strategy.
For students who correctly answered the number of counters and showed a counting strategy, encourage them to find a quicker way of working it out – use questions 2 and 3 above to guide them to finding a non-counting strategy.
Encourage students to look at the range of different strategies used by the group/class and discuss which are more efficient and accurate.

Strategies
Students who used multiplicative strategies to solve the problem were more successful at getting a correct answer – indicating both a higher maths ability and also a more robust, usable strategy.
A counting strategy can be more prone to miscounting errors, or taking significantly more time to solve.

For a similar resource about arrays and additive strategies see Cover up.
 
Numeracy links
The strategy the students employ and show to solve the questions in this resource can be an indicator of students who are still using counting-by-one strategies (Stages 1-3, Numeracy Framework) and those developing more advanced counting (Stage 4), or part-whole strategies (for addition, subtraction, and multiplication – Stages 5-6).