Decimals on number lines
|
|
a) Show where each of the decimal numbers go on the number line below.

b) Show where each of the decimal numbers go on the number line below.

| Y6 (06/09) | ||
| a) |
Decimal fractions placed in approximately correct position. 0.8 0.25 0.65 
All 3 correct
2 correct |
very difficult |
| b) |
Decimal fractions placed in approximately correct position. 1.2 0.9 0.45 
All 3 correct
2 correct |
difficult very difficult |
In assessing whether students can place decimal numbers on a number line, this resource explores three ideas:
- ordering decimals,
- placing decimals on a number line
- comparing decimals with different numbers of decimal places.
Prior knowledge
Working with number lines and how to plot between points on a number line.
Place value of decimal parts of a number up to 2 decimal places.
Decimal place value understanding
By being able to solve these questions correctly students can be showing a deeper understanding about the size and a place value of decimals up to 2 decimal places (d.p).
Students may be able to order decimals with the same number of decimal places, but when comparing decimals with different numbers of decimal places they may revert to their whole number knowledge. For example using money to explore decimals has this shortcoming (as cents are both whole number cents and decimals of dollars). This all highlights the importance of varying the number of decimal places when assessing students' understanding of decimal place value.
Having a number line also means that there is an element of justification of not only ordering numbers but placing them while considering relative magnitudes of difference (density of decimal numbers).
A misconception that underlies many errors that students made is reverting to treating the decimal number as a whole number (e.g., 0.65 becomes 65). This error tends to emerge when the decimal places are different [e.g., 0.345 becomes 345 and is therefore larger than 0.65 (65)].
Common errors and misconceptions
Whole number error
About one-sixth of students indicated the type of solution below, where 0.8 was shown as larger than 0.5 (but not accurately) and 0.25 and 0.65 were placed after 0.8. Here it is likely that the decimal numbers were seen as the whole numbers 8, 25, and 65, and that 0.5 was 5.

This is similar for question b) where the student solution on the number line may look like:

Whole number with adjustment error
Other students answered similarly to the above error, except that they placed 0.8 where 0.08 would go.
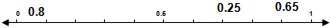
"swap" 0.9 and 0.45 because of a whole number interpretation of the numbers: comparing 9 and 45. Note that 0.45 and 0.9 were swapped, but 0.45 was not often marked correctly. About one-sixth of students gave a similar solution to this in question b).

This error was particularly noticeable with marking the location of 1.2 in question b). Almost a third of students marked the second mark from 1 – 2 which was actually 1.4. Another similar common error was when the number indicated is between two marks. For example, 0.45 needed to be marked between two marks (0.4 and 0.6), but also more toward 0.4 to indicate it is less than 0.5.
Many of the errors students made involved reverting back to whole number values. For students who exhibited this misconception, it may be more important to first get them to simply work with physical representations (abacus, 100 blocks, decimal pipes, decimal arrow cards, decimats, decimal fraction mat) of decimal numbers with different number of decimal places and then discuss what decimal place value means. Students could then explore problems about ordering decimal numbers without the number line.
Using number lines
After students can order decimal numbers with different numbers of decimal places, students can look to plotting them on a simple number line justifying their placement.
The early use of number lines (decimal number lines) to represent decimals can also support place value understanding. This means that students become more familiar with a number line and can use it to promote understanding concepts through multiple representations rather than the number line being something they must also learn on top of decimals.
Correctly labelled all decimal numbers (extension)
For students who could correctly label all three of both sets of decimal numbers, they could also be asked to identify a decimal number between two given decimal numbers (e.g., name a decimal number between 0.65 and 0.8 (or 0.65 and 0.652) and show where it would go on the number line.
Students could also be asked to indicate the same decimal number on number lines with different scales and different gradations (e.g., number lines ranging from 0-4, 4-5, 0-3 with gradations of 0.5, 0.1, 0.3 respectively, and with arrows both sides indicating how the number line continues forward and backwards).
Developing understanding of decimal density
The marks on the number line can also be removed and students can use measurement and estimating skills to determine decimal number locations. This all supports students understanding of the density of decimal numbers as well as their understanding about decimal place value and size.
Book 7: Teaching fractions, decimals and percentages, (Stages 6-7: Advanced additive/Early multiplicative - Advanced multiplicative)
- Pipe Music with decimals (adding and subtracting decimal numbers)
- Deci-mats (naming decimals from fractions)
- Using: decimal arrow cards, decimats, decimal fraction mat and decimal number lines.