Different fractions on a number line

Different fractions on a number line

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about ordering fractions.

 

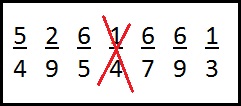
Using the fractions in the box above, write the fractions in their correct positions on the number line below.

\(1 \over 4\) has been done for you.

 

Task administration: 
This task is completed with pencil and paper only.
Level:
4
Curriculum info: 
Maths, Number and Algebra, Number Knowledge
Keywords: 
fractions, number lines, improper fractions, ordering fractions
Description of task: 
Students order a range of fractions on a number line.
Answers/responses: 
  Y8 (11/07)

In order from left to right:
2/9
1/3
6/9
6/7
6/5
5/4
All 6 fractions in order

2/9 , 1/3 , 6/9 , 6/7 , 6/5 , 5/4

One error, e.g.,

2/9 , 1/3 , 6/9 , 6/7 , 5/4 , 6/5 or 2/9 , 1/3 , 6/7 , 6/9 , 6/5 , 5/4 or 2/9 , 6/9 , 1/3 , 6/7 , 6/5 , 5/4

 moderate
easy
difficult
moderate
difficult
difficult

difficult


moderate

Based on a representative sample of 163 students.

NOTE: An error can be a transposition of two fractions, an omission, or a fraction written incorrectly.

Teaching and learning: 
This resource requires students to place non-unit and improper fractions on a number line.  There are two aspects to this resource: location of the fraction on the number line and order of the fraction in relation to the other fractions.  This resource indicates more than an understanding about the relationship between the numerator and the denominator (part-whole), it explores the idea of fraction size and the idea of fractions as numbers that can be shown on a number line.  
The important ideas in this resource are being able to recognise and place:

  • fractions with the same numerator and different denominator
  • fractions with a denominator that is a factor or multiple of another
  • improper fractions (also called top heavy fractions, where the numerator > denominator).
Diagnostic and formative information: 
About one quarter of students identified 6/9 as the largest fraction, and a similar number identified 1/3 as the smallest fraction.  Students who cannot order these fractions are likely to be using an understanding of whole numbers to try to order the fractions, rather than an understanding of fractions as being numbers. 

Over half of the students recognised that 6/5 and 5/4 were improper fractions and therefore greater than 1.  However, some of these students indicated that 6/5 was greater than 5/4 – suggesting a whole number influence on their thinking.

Common error Likely misconception
1/3 , 5/4 , 6/5 , 6/7 , 2/9 , 6/9
(denominator then numerator)
1/3 , 2/9 , 5/4 , 6/5 , 6/7 , 6/9
(numerator  then denominator)		 Ordering by denominator and then numerator (or vice versa)
Students have a misconception about the relationship between the denominator and numerator.  They try to relate the two numbers by ordering by numerator first, then using denominator (or vice versa) to determine the final order.
1/9 , 5/3 , 2/9 , 6/7 , 6/5 , 6/4 Whole number misconception (application)
Students combine the top and bottom number in some way and order them as whole number values. Students may be applying the rule: "the larger the numbers the larger the fraction".
2/9 , 1/3 , 6/9 , 6/7 , 5/4 , 6/5 Transposing improper fractions
Students order most of the fractions correctly but revert to a whole number understanding to order 5/4 and 6/5 (i.e., 6 & 5 are larger than 5 & 4).
Next steps: 
Whole number misconception (application) or ordering using denominator and numerator separately
Students who have misconceptions that involve using whole number rules or ordering by denominator and numerator separately, need to develop a part-whole understanding of fractions before trying to devise a system to order or compare fractions.  This is about recognising that a fraction is a part of a whole, and that it is the relationship between the top and bottom number that describes and quantifies the fraction, i.e.,  it is about the relationship between the numbers, not their absolute size. 

If required, students could go back to partitioning and explore constructing the parts (unit fractions), then combining these parts to make up and name fractions.  Encourage students to explore a range of less familiar fractions such as 3/13 , 11/27 , etc, and some improper (top heavy) fractions and discuss how large these fractions are.  After this, encourage students to compare just two fractions before trying to order a number of them.  Appropriate drawing of fractions can promote understanding and help with comparing the size of fractions.

Transposition of two fractions, omission, or fraction written incorrectly
For students who misplace 1 or 2 fractions, ask them to explain how they know that the misplaced fraction is larger or smaller and to show this using a diagram.  They can begin by partitioning a rectangle, showing each fraction, and then comparing them.  For a resource about comparing fractions see NM0138: Larger fractions (level 3).

Not recognising improper fractions
For students who did not recognise 5/4 and 6/5 as being greater than 1, draw another number line, partition the number line into appropriate unit fractions and build up the non-unit fractions and improper fractions, e.g.,     1/5 , 3/5 , 6/5 ; 7/5 … or 1/4 , 3/4 , 5/4 ; 7/4 , etc.

Correct placement of all six fractions
For students who could place all six fractions correctly, use a number line between 0 and 2 and explore a range of improper (and mixed) fractions, showing where they think they might go.

 
Numeracy resources
Book 7: Teaching Fractions, Decimals and Percentages, 2006:
Fraction circles, (p.9), Advanced counting/early additive part-whole
Trains (p.19) Early additive/Advanced additive/Early multiplicative.