Close to one

Close to one

Pencil and paperOnline interactive
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about identifying how close some fractions are to 1.

Question

a)  Select all the fractions that are larger than 1. 

    • \(3 \over 4\)

    • \(6 \over 5\)

    • \(7 \over 8\)

    • \(7 \over 9\)

    • \(9 \over 8\)

    • \(9 \over 10\)

Question 1Change answer

b)  Explain how you can tell when a fraction is larger than 1.

Question 1Change answer

c)  How far away from 1 is each of these fractions? 
     Write your answer as a fraction.
\(3 \over 4\)   
\(7 \over 9\)   
\(9 \over 8\)   
Task administration: 
This task is completed with pencil and paper or online.
Level:
4
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Key Competencies: 
Using language, symbols, and texts
Keywords: 
fractions, improper fractions, subtraction, ordering fractions, key competencies
Description of task: 
Students identify fractions that are greater than one, explain their reasoning and identify how far from one some fractions are.
Curriculum Links: 
This resource can help to identify students' ability to apply strategies to solve subtraction problems involving fractions.
Key competencies
This resource involves explaining why a fraction is greater or less than 1. This relates to the Key Competency: Using language, symbols and text.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Additive thinking, sets 7-8
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
  Y6 (06/2009)
a)

 

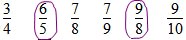 difficult
b)

 

 Explanation involving that the top number (numerator) is greater than the bottom number (denominator):
For example

  • the top number is more than half than the bottom number.
  • other sufficient explanations/diagrams justifying their answer.
 difficult
c)

i)
ii)
iii)

1/4 or 1 quarter
2/9
1/8
Note: as well as the size of the difference some students also indicated whether the fraction was greater or less than one.

difficult
difficult
very difficult
Based on a representative sample of 179 Y6 students.
Teaching and learning: 
This resource is about being able to work out whether fractions are less than or greater than one, and by how much (closeness).  Being aware that fractions can be greater than one (or two, three, etc.) is an important understanding that moves students' understanding towards fractions as numbers with size and comparability.

Prior knowledge
If students are not aware of fractions as a relationship between a part and a whole, they may have difficulty identifying how the numerator and denominator are used to work out the size of a fraction, and may try other relationships, such as subtraction, addition, or "the largest" of the numbers.

Diagnostic and formative information: 
  Common error Likely misconception
a)

b)

 6/5 , 7/8 , 7/9 , 9/8 , 9/10 Whole number misconceptions
Larger numbers mean larger fractions
The numerator of 9 is the highest number.  Fractions can be misconceived as less than one and if they are larger than one they would be the larger numbers. (Over a third of students thought 9/10 > 1)
Fraction notation is two separate numbers
Students treat the fraction as two separate numbers and describe some other system of attempting to judge fraction size from these numbers, e.g., the fraction value is the difference between the bottom and top number (7/10 has a value of 10–7=3), or the fraction value is the sum (7/10 has a value of 10+7=17).
c) 1 (piece),
2 (pieces/ quarters)
1 (pieces/ quarters)		 Writing the number of pieces (or "quarters") rather than the fraction
Students refer only to the number of pieces away from one not their size. A derivation of this was when students called their pieces "quarters", but meaning "pieces". This may indicate a further misunderstanding about naming fractions.
b)


c) iii)

 None (are larger
than 1)

Already one
0, 0/0 , 0/2 ,or 0/8

 All fractions are less than or already one
Students indicate that none of the fractions are greater than one.  This relates to the misconception that "all fractions are less than one".

Students identify that the fraction is already one or equal to one.
c) iii) 1/9 Incorrect denominator for difference
One less piece, but uses the top instead of the bottom number as denominator for the difference.
c) iii)

 

c) i)
ii)

 8/7

 

7/4
3/9 or 3/1

 Does not know how to add or subtract to one with fractions
One less piece error (problems with fraction notation)
One less piece, but reduces top and bottom numbers by one to show the new fraction.
Make to 10 error
Make to 10 with the top number,
e.g., question c) ii) 7/9 + 3/9 = 10/9 (adding top numbers with common denominator), or
7/9 + 3/1 = 10/10 (adding top and bottom numbers – as two whole numbers)
Next steps: 

Whole number misconceptions
Students who either treat the fraction as two separate numbers, or indicate that the larger the numbers the larger the fractions are likely to not recognise that fractions are a different kind of number (rational numbers), and may need to develop a part-whole understanding of fractions before trying to compare fractions.  Ultimately the relationship between top and bottom numbers is a division relationship. Students may benefit from looking at the part-whole representation of fractions through partitioning exercises, drawing fraction diagrams (Shaded fractions and Fraction shapes), and comparing fractions using diagrams to identify what constitutes the size of a fraction.  For example, students could show how much 6/9 and 4/5 are,

They could talk about the size of the pieces and how many there are in each fraction. Students may also need to explore improper fractions by adding a number of additional parts or counting up sequences of parts beyond 1, e.g., 2/5 , 3/5 , 4/5 , 5/5 , 6/5 , etc.  This could be supported by using number lines to show fractions. Students could also look at questions involving fraction diagrams of improper fractions, and identify what part and what whole shape they are working with (e.g., Parts and wholes and Cuisenaires and fractions ).
Asking students what the whole shape is, and then what part they are finding, can support them to develop a more part-whole understanding about fractions. This could also be supported by using a number line to show where fractions fit in between whole numbers.

Writing the number of pieces rather than the fraction
For students who gave the number of pieces as their answer, encourage them to find out what fraction (or a way to find out how large) the pieces are and incorporate that into their answer, e.g., for 3/4  students could draw the shape and identify the size of the fraction needed to complete to the whole.

All fractions are less than one
Students who indicated that some fractions were already one (in question c), no fractions were larger than one (in question a and b) or could not explain how to tell when a fraction is larger than one may need to explore improper fractions.  Students could go back to partitioning and explore constructing the parts (unit fractions), combining these parts to make non-unit fractions that are between 0 and 1 (also called proper fractions), naming these new fractions (part-whole fractions), and then exploring improper fractions by counting up sequences of parts beyond 1, e.g., 2/5 , 3/5 , 4/5 , 5/5 , 6/5 , etc.  This could be supported by using a number line.  Students could then be asked to quantify how far each fraction is from one.

Does not know how to add or subtract to one with fractions
Most of the above common errors involving writing incorrect fractions could be addressed by getting students to draw the fraction they are considering and use the given denominator to also draw a half.  For example, How far away from one is 3/4 ? Students could draw 3/4 indicate the difference, then quantify the size of the difference.

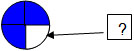
Students could then look at the denominator and numerator to identify any pattern (that the difference is 1/4 (which is 1 – 3/4).  This example could be followed by the modelling of the difference to one of an improper fraction, explicitly noting the whole and what "part" is being compared, e.g., if the whole was we want to know what fraction is, and how far it is from one whole.  It is 1 whole and a third, so 1/3 more than one.

Using decimals
Some students might prefer to compare fractions by first converting them into decimals.  They will often rely on a calculator to do this.  It is important to challenge them to look at how using information about the denominator and numerator could be used.

Whole class discussion
Many of the above next steps can be explored in whole class discussion where students share and critique their own and others' strategies to develop a fuller understanding.
For more information about comparing fractions, and fractional thinking, see the Fractional Thinking Concept Map: equivalence.
 
Numeracy resources
Book 7: Teaching Fractions, Decimals and Percentages, 2006
  • Trains (Early/Advanced additive)
  • Wafers (Advanced counting/Early additive)