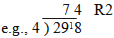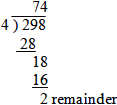Left over toys

Left over toys

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about equal sharing with a remainder.

A toy company distributes a range of toys to shops. The shops need to get equal numbers of toys. Sometimes there are toys left over. This is called a remainder. The toy company needs to know:

  1. how many toys each shop gets; and
  2. how many toys remain (if there are any).
a) Show how you could divide 298 trolleys equally between 4 shops

Answer: __________  
 
b)
 
Show how you could divide 629 tricycles equally between 6 shops.

Answer: __________  
 
c)
 
Show how you could divide 567 robots equally between 8 shops.

Answer: __________  
 
d)
 
Show how you could divide 347 aeroplanes equally between 7 shops.

Answer: __________  
Task administration: 
This task is completed with pencil and paper only.
Level:
4
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Key Competencies: 
Using language, symbols, and texts
Keywords: 
division, partitioning, equal sharing
Description of task: 
Students show how to divide 3-digit whole numbers into equal sized groups and identify any remainder.
Curriculum Links: 
This resource can help to identify students' understanding of division. A possible progression for understanding could involve: 
  • use of remainders in this resource and also the nature of the resource encourage the use of a number of multiplicative strategies, (Advanced multiplicative, Stage 7)  
  • use of multiplication and division as inverse relationships. Many students showed this on their scripts when they re-checked their working by reverse multiplying.
  • simple place value partitioning (or an additive strategy) without discernment for the numbers. 
Key competencies
This resource involves recording the strategies students use to solve division problems. This relates to the Key Competency: Using language, symbols and text.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Multiplicative thinking, sets 6-7
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
  Y8 (11/2009)
a) 74 and 2R or 74.5 or 74 1/2 . Working involving the following strategies:

  • Place value partitioning:
    200 ÷ 4 = 50; 90 ÷ 4 = 22.5 (R2); 8 ÷ 4 = 2; 50 + 22.5 +2 = 74.5
  • Other partitioning strategy (tidy numbers, compatible numbers),
    200 ÷ 4 = 50; 98 ÷ 4 = 24.5 (or remainder 2); 50 + 24.5 = 74.5
  • Short division:
  • Rounding then compensating:
    298 rounds to 300 (2 difference); 300 ÷ 4 = 75 then compensate by removing the 2 difference (from 2 of the shops), which means that there is 74 each and 2 remainder.
  • Partitioning based on factors:
    Recognising that c) 280 divides by 4 (70 times) with 18 left over (18 divides into 4 four times with 2R; 70 + 4 with 2R;
  • Halving: halving 298 to 149, and then again to 74.5
  • Long division:
  • Physical representation:
  • Other trial and improvement, or counting strategy
moderate
easy
b)

104 and 5R or 104.83 or 104 5/6
And working involving strategies as above.

moderate
easy
c)

70 and 7R or 70.875 or 70 7/8
And working involving strategies as above.

moderate
easy
d)

49 and 4R or 49.57 or 49 4/7
And working involving strategies as above.

moderate
easy
Based on a representative sample of 156 Y8 students.
Teaching and learning: 
These questions are about dividing larger 3-digit numbers into a number of groups.  The questions involve remainders.  Many of the numbers have been selected to encourage exploration of part-whole division strategies that involve pulling numbers apart and rejoining as required.  The first question invites a halving strategy with adjustment.

Prior knowledge

  • Understanding about division operations.
  • Multiplication basic facts (also division basic facts)
Diagnostic and formative information: 

Strategies
Students used a range of strategies to solve these division problems: short division, long division, place value partitioning, other partitioning strategies (e.g., rounding and compensation, identifying appropriate factors, compatible numbers), physical representation, and trial and improvement. The most common strategy was short division, followed by a range of part-whole partitioning strategies. The more discerning partitioning strategies utilised the numbers and tended to be more accurate than simple place value portioning. However the long (85%) and short division (72%) were the most accurate strategies along with the visual partitioning (80%).  Interestingly, the students who used the visual partitioning (place value) had the highest mean ability – this may relate to the fact that the question asked "to show" their working and this strategy shows how numbers can be partitioned. The mean ability of students who used short division was higher than all the remaining strategies – including long division.

  Common error Likely misconception
b)
c)		 14R5 or 140R5
7R7 or 77		 Place value error when dividing. 
Students do not put a zero after attempting to divide 6 into the 2, or 8 into the 6 (of 569).
a)
b)
c)
d)		 74 (75)
104 (105)
70 (71)
49 (50)		 Answer does not include the remainder
Students do show what happens to the "bit left over" after the division.  Most responses were truncated.
Next steps: 
Students who did not show their strategies because they did not know where to start.
They need to be working with materials or using smaller more workable numbers to explore what division is. The resources Sharing counters, Equal sharing III, and Equal sharing II all explore equal sharing at level 2 (the last two require students to show their working.  At level 2 strategies used may be counting out, 1-1 matching, skip counting, repeated addition or some other additive strategy.

Students who used short division and came up with an incorrect answer. 
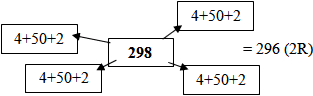
What is important, before using this procedure for division, is that students understand what division does to numbers.  Therefore it would be helpful for them to explore using the visual partitioning (shown below) to solve some division problems and then some other type of partitioning strategy.  These will develop an understanding of how the short division can work.  Also getting student to check their work (as some did) by multiplying their answer (quotient) with the divisor and looking for any differences.

Students who used part-whole partitioning (including place value partitioning) and came up with an incorrect answer
Students should set up the place value partition (for starters) graphically and apportion out the partitions for each place value factor of 10. For example:

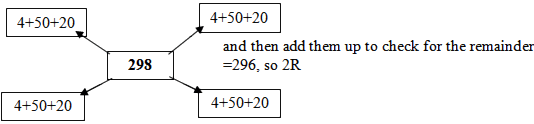
Student who used counting or additive strategies. 
Get them to share their strategies in a small group or whole class discussion and start to identify more efficient strategies that do not require as much time. Also look at the most appropriate strategy for the numbers in the questions (for example, looking for factors before deconstructing the numbers).  For question a) a simple strategy was to halve the number twice to get the answer.  The other questions involved identifying some basic facts relationships

Students who did not include the remainder (as a remainder, fraction or decimal). 
These students should be asked to check to see if there was any left over when they solved the question. They could also check their answer by reverse multiplying to see if there is any difference (remainder). After they are comfortable with the remainder, students need to develop the awareness of the relative value of the remainder – as we have divided the whole number (quotient) by the divisor, the remainder should also divided by the divisor, and left as a fraction, e.g., 567 ÷ 8, after dividing 560 by 8 (divisor), would result in 7 remainder – this can be divided by 8 to get 7/8 as the fraction component of the division. The same idea behind part-whole nature of numbers (whole and rational) means that the fraction can be separated and operated upon, and then re-attached.

Students who did not show their strategies.
They may not be aware of why it is important, they may have not been required to do so in the past or they may not know where to start. These students could be given examples of the question and peoples' incorrect strategies and asked how to work the correct answer. Having students identify or write their strategies down reveals their understanding or misconceptions and can be analysed to work out next steps.

Appendix - Strategies

Strategies question a question b question c question d overall accuracy across 4 questions
Place value partitioning strategy 11 (3) 11 (4) 5 (0) 6 (0) 7/33 = 21%
Other partitioning strategies 10 (6) 15 (7) 8 (1) 7 (3) 17/40 = 42%
Recognising and using the factor 12 (10) 10 (5) 14 (10) 14 (9) 34/50 = 64%
Short division 58 (45) 54 (32) 57 (39) 57 (46) 162/226 = 72%
Long division 5 (4) 5 (5) 5 (4) 5 (4) 17/20 = 85%
Visual partitioning/ place value splitting 11 (8) 12 (11) 12 (9) 10 (8) 36/45 = 80%
No strategy (answer given) 23 (9) 22 (4) 26 (5) 21 (1) 19/92 = 21%

Based on a representative sample of 156 Y8 students. Key = Number of students who answered strategy (number of correct answers using strategy)

Links to the Number Framework
The strategies that students use can help determine their stage of development within the Number Framework.  Strategies that could be used for this resource include one-to-one mapping, visual grouping, (partitioning and trial and improvement), repeated addition/subtraction, skip counting, multiplication, and division.  Students using additive strategies are indicating Stage 5 (Early additive) strategies, and students using multiplicative strategies are indicating Stage 6 (Early multiplicative). If students can use a range of multiplicative strategies they are considered to be at stage 7 (Advanced multiplicative).