Parts and wholes

Parts and wholes

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about fractions of shapes.
a)  
 is  \(1 \over 4\) of the whole shape.
i) What fraction of the whole shape is  ? ________
                                                                        
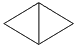ii) Draw what \(3 \over 4\) might look like.
 
 
iii) What fraction of the whole shape is  ? _________
 
b)  
\(3 \over 4\) of all the counters is 

i) Draw the whole set of counters.
 

 
 
 
ii) Show how much \(1 \over 4\) of the whole set would be.
 
 
 
c)  
 is \(4 \over 5\) of the whole shape.

i) What fraction of the whole shape is  ? ________

ii) Draw what the whole shape might look like.

 
 
 

 
iii) Draw what \(7 \over 5\) might look like.
 
Task administration: 
This task is completed with pencil and paper only.
 
Level:
3
Curriculum info: 
Maths, Number and Algebra, Number Knowledge
Keywords: 
fractions, part-whole fractions, unitising
Description of task: 
Students show that they can picture the whole shape when given a fractional part.
Curriculum Links: 
Key Competencies: Thinking
This way of asking part-whole fraction questions challenges a learned "process" for solving such questions, and requires flexible thinking to make sense of the information given as the referent whole changes for each question. Key competencies: Thinking.
Answers/responses: 
  Y6 (11/2006)
a)
i)
 
ii)
 
 
 
iii)
2/4

 

or any other variation with 3 triangles.
 
3/2 or 11/2 (or any equivalent amount including 1.5)
easy
 

moderate

 
 
 

moderate
b)
i)
 
 
 
 
 
ii)
[Showing 16 counters]

[Showing 4 counters]

[Some students incorrectly answered b) i), and then found 1/4 of i). This is marked as correct for b) ii)]
moderate
 
 
 
 
 
easy
c)
i)
ii)
 

iii)
1/5
moderate
moderate
 

moderate
Based on a representative sample of 161 Y6 students.
Teaching and learning: 
This resource explores students' ability to think about part-whole fraction problems differently.  Instead of being shown a whole shape with a shaded part and asked what fraction is shaded, students are given a shape and told what fractional value it represents. They are then asked to find another fractional part or the whole (referent whole).  This requires them to use the information given to think dynamically about the relationships between the part and the whole rather than simply naming a shaded part from a given whole.
 
In this activity students demonstrate their understanding of fractions by showing that they can relate a given part to a whole, or another different part.  These questions challenge the convention of just asking "what is the fraction of a given whole?"  Changing the way these questions are asked reduces the chance of students developing procedures without understanding.
 
Diagnostic and formative information: 

A significant number of students changed what the whole (called referent whole) was that they were finding fractions of. This misconception underlies a range of errors.

  Common error Likely misconception
c) i) 1 Whole number misconception
Students identify that the shape is one piece and may not understand how to construct a fraction.
a) i) 1/8 Students double the denominator (not double the fraction).
b) ii) &
c) ii)

a) ii)
Another representation of the same fraction,
e.g., a whole  or 3/4 
 Using icons to represent fractions
Students may have a standardised picture of what a fraction looks like and that is what they show.
a) iii) 1/6 Changing the referent whole
Students regard the shapes as the whole and name one part of it rather than still treating the one triangle as 1/4 .
a) iii) 6/6 , 6/7 , 6/8 Students count 6 parts in the shape but lose track of what the whole is when they try to construct a fraction.
c) i) 1/4 Students regard the square as a part of the four squares and ignore that the fours squares are 4/5 of the whole – not the whole.
Next steps: 
Whole number misconception
Students who write their answer as a whole number may need to develop an understanding about what a fraction represents, i.e., that if a set is partitioned equally into n parts then each part is called 1/n .  Students need to have more experience partitioning and naming the unit fraction/parts they have created [click on the link Fractional thinking concept map, and go to the section Partitioning and divided quantities].
Students beginning to understand fractions should be encouraged to use words to describe the parts, and delay the fractional notation until they have developed some understanding of fractions as relationships between a part and a whole [click on the link Fractional thinking concept map, and go to the section on Fractions as part-whole relationships].

Icons to represent fractions – not using the same (referent) whole
Some students may have only a limited exposure to representation of fractions and may not realise there are many ways to show a fraction and that the fraction describes a relationship between a part and a whole.  For example, if students have only ever seen fractions in round pizza shapes when they are asked to find 3/4 of any other whole they have a strong visualisation that 3/4 is shaded-shape-6.png and cannot find 3/4 of the whole given.

For this understanding about fractions as relationships between the parts and the whole it is important to have one common whole and the answer should be given for the same referent whole.
For example, if asked to show 3/4 of shape-7.png the answer: shaded-shape-6.png does not relate to the initial whole.

Whereas the answer: shaded-shape-8.png does relate to the initial whole and is therefore a more suitable representation of the fraction 3/4 of that referent whole.

Changing the referent whole
This is similar to the above misconception except it involves a more explicit change or complete lack of recognising what whole we are finding the fraction of.  With this type of question students are given a part and required to either find a whole or another part. 
Two ways to finding another part are:

  1. Building up to the whole and then finding the new part of that whole, finding the whole example [click on the link Fractional thinking concept map, and go to the subsection on Finding the whole from a part].
  2. Recognising the relationship between the two different parts, finding parts example [click on the link Fractional thinking concept map, and go to the subsection on Using the part to find another part].

Working with diagrams and physical objects can help students use their intuition.  As they move on they can still be encouraged to imagine a physical object or draw pictures to help them (imaging).  Encourage students to verbalise the strategies they use to work out the answer.  Often students can identify and share more than one way of getting to an answer.

For more information on fractions as part-whole relationships, click on the link Fractional thinking concept map, and go to the section on Fractions as part-whole relationships.