Dividing squares
| a) |
i) Show 3 different ways of dividing a square into 2 equal parts.
   |
|||||
|
ii) Name the fraction that one of the pieces above shows. _____ |
||||||
| b) |
i) Show 3 different ways of dividing a square into 4 equal parts.
   |
|||||
|
ii) Name the fraction that one of the pieces above shows. _____ |
||||||
| Y4 (11/2006) | ||||
| a) |
i)
ii)
|
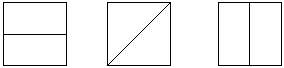 or other acceptable partitions.
1/2
|
very easy
(all 3 correct)
or very easy
(for two correct & none incorrect)
easy
|
|
| b) |
i)
ii)
|
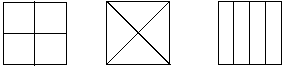 or other acceptable partitions.
1/4
|
moderate
(for all 3 correct)
or easy
(for two correct & none incorrect)
moderate
|
|
 and
and  .
. | Common error | Likely misconception | |
|
a) ii) b) ii) |
2 4 |
Whole number The number of parts is given as the answer indicating that they either do not know what a fraction is or do not know how to construct one. |
|
a) ii) b) ii) |
2/2 4/4 |
Relationship between the top and bottom number of a fraction
Students attempt to construct a fraction – but do not have a part-whole understanding about the relationship between the top and the bottom number.
This is similar to the whole number misconception except that students are aware of the notation style of a fraction, a/b.
|
For students who had difficulty partitioning into the shape into even parts. Give them opportunity to use folding or cutting to divide up shapes and encourage them to explain how they know the partitions are even, and how they could justify this to somebody else.
For students who could only show two ways to divide up the shapes. The most common partitions they showed were:  and
and  .
.
They could be further supported by asking "what other ways could they be cut up?" (What if it was cake or a loaf of bread how would we cut it up?)
For students who could show three ways to partition the shapes. It is important that students further develop their experiences of partitioning starting with:
- halving of basic shapes, then halving multiple times to derive other parts;
- partitioning a variety of shapes: squares, two squares, rectangles, circles, hexagons (which may be easier to partition for younger students), etc.;
- partitioning shapes into a different number of pieces (e.g., 3, 5, 6, 7, 9, etc).
By partitioning shapes into an odd number of parts and by using a number of shapes, students can develop a more robust understanding of partitioning. This variety ensures that they are not just memorising how to partition certain shapes, but they have the ability to partition any simple shape and understand the importance of these parts being equal-sized.
Misconceptions about naming fractions (part-whole relationships)
Students who write their answer as the count of the number of parts (whole number) need to develop an understanding about what a unit fraction represents, i.e., that if a shape is partitioned equally into n parts then each part is called 1/n. Students need to have more experience partitioning sets and naming the unit fraction/parts they have created. Students beginning to understand fractions should be encouraged to use words to describe the parts, and delay the fractional notation until they have developed some understanding of what fractions represent.
Students who write their answer as the number of parts as both the top and the bottom number have developed some understanding about fractional notation, but still need to develop an understanding of how fractions are named (see above).
Show some examples of shapes with simple parts shaded and ask what fraction of the shape is shaded. Encourage students to recognise the relationship between the number of equal-sized pieces the shape is partitioned into (denominator) and the number of these parts of interest (numerator). It may be helpful to remind students to ask themselves "What is the whole shape?" (referent whole) and "How much of the shape is each part?".

