Sharing counters

Sharing counters

Auto-markingPencil and paperOnline interactive
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about sharing out a set of counters into equal sized groups.
Counters-for-sharing-counters-1.png
You will need 30 counters for this task. 

Question 1Change answer

a)  Put 12 counters in front of you.
     i)  Make 3 groups of equal size.
           How many counters are in one of these groups?  

     ii)  If the 12 counters were put in 6 equal sized groups, how many counters would be in one group?

Question 1Change answer

b)  Put 24 counters in front of you.
     i)  Make 4 groups of equal size. 
           How many counters are in one of these groups?  

     ii)  If the 24 counters were put in 8 equal sized groups, how many counters would be in one group?

Question 1Change answer

c)  Put 30 counters in front of you.
     i)  Make 6 groups of equal size. 
           How many counters are in one of these groups?

     ii)  If the 30 counters were put in 10 equal sized groups, how many counters would be in one group?

Question

d)  20 counters have been made into 4 equal-sized groups.
20 counters
     What fraction of all 20 counters is one group?

    • \(1 \over 5\)

    • \(1 \over 2\)

    • \(1 \over 4\)

    • \(1 \over 3\)

Task administration: 
This task can be completed with pencil and paper or online (with auto marking displayed to students), other equipment is required.
 
Equipment: 30 counters of the same colour per student.
  • This resource is designed for small group work, where the teacher can observe how students set up and partition the sets.
  • How students partition is an important part of this resource.  It can identify students that are using counting strategies to solve sharing problems.
  • Make a note of students who set up the counters as arrays, single lines or clusters.
  • Ask students if they can identify other equal-sized groups they could put the counters into.

NOTE: The questions ask students to partition a set into a number of groups.  Dividing counters into groups of a given size and asking how many groups is a different type of division, called quotition.  For example "How many groups with 2 counters in them could you make with the counters?"

Level:
2
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Keywords: 
fractions, partitioning, equal sharing
Description of task: 
Students share out sets of counters into equal-sized groups.
Curriculum Links: 
This resource can help to identify students' ability to use basic facts and knowledge of place value and partitioning whole numbers to solve partitive division problemS.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Multiplicative thinking, sets 3-4
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
 
a) i)
ii)		 4
2
b) i)
ii)		 6
3
c) i)
ii)		 5
3
d)   1/4
Results based on a trial set of 30 Y4 students.
Teaching and learning: 
Partitioning is an important understanding that lies at the heart of understanding fractions, percentages and decimals.  It involves dividing an object or set of objects into a given number of non-overlapping parts.

NOTE: Encourage students to use the word fraction rather than part, as future fraction problems may ask for top heavy (or improper) fractions, e.g., 5 quarters, which is not so intuitively a "part".

Diagnostic and formative information: 
The methods students use to partition a set of objects is as important as whether they can actually partition.  Some strategies are based on counting and matching, whilst others support multiplicative understanding, such as: arranging as an array; or knowing that the partitioning involves division, working out the group size and then breaking into groups of a known size.
Next steps: 
Not sharing equally
For students who cannot use a strategy to share the counters equally, introduce the idea of sharing amongst people and what would be fair.  Ask “Is someone getting more than someone else?”.  Explore this equal sharing with shapes and sets of countable items.  Encourage students to think about how to lay them out to make breaking them into groups easier.  Start with small numbers divided into small groups, e.g., 6 counters into 2 groups, and then ask them to explain how they worked it out.  Then suggest they use this same strategy for larger numbers of counters and groups.

Using a counting strategy
Students who line the counters up and count out the counters into the groups then count the number in each group are using a counting strategy, e.g.,

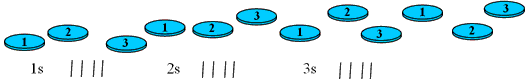
This indicates that they understand the concept of equal-size and equal sharing (see resource Equal sharing with countable items).
Once they can use this strategy successfully, encourage students to think about other strategies to share the set of objects between the groups without counting.  For example, using an array may help students visualise the groups that make up a set, or asking children what they know about the number of counters in the set and number of groups required, e.g., "If there are 12 counters and 3 equal-sized groups, what do we know about breaking 12 into 3 parts?"

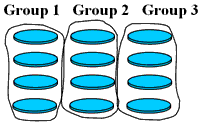
NOTE: After students can arrange counters to solve equal sharing problems, encourage them to visualise the counters in their head without needing the counters (called imaging).

Sharing equally
For students who can share the set into n parts and identify the division relationship of partitioning, ask them to name what fraction one part of the set is, e.g., "what fraction of the whole set is one of the groups?"
Students may know that 12 into 3 groups is
12 ÷ 3 = 4
which means there is 4 in each group

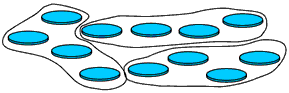
This encourages students to recognise that a fraction is a part of a whole (part whole understanding of fractions).  This whole can be a set, a region or a number.

For more information about partitioning and fractions see the Fractional thinking concept map.
 
Links to Numeracy
Equal sharing of sets, numbers or regions for simple problems and using a matching strategy is at Stage 4: Advanced counting - Stage 5: early additive part-whole.  Students who can construct and name non-unit fractions are at Stage 5: early additive part-whole (using repeating addition) - Stage 6: Advanced additive (partitioning using division) part-whole.