Cutting up

Cutting up

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about cutting a square and a circle into equal parts.
 
 
1)

 
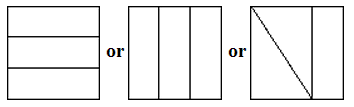
Alli drew lines to divide this square into 3 equal-sized pieces. 
 
a)  Are all 3 pieces equal-sized?  yes  /  no  /  don't know  (Circle one)
 
 
 
 

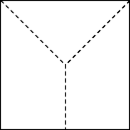
b)  Show how you would divide the square into 3 equal-sized pieces.
 
medium-sized-square.png
 
2)

 
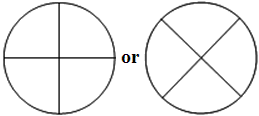
Josef drew lines to divide this circle into 4 equal-sized pieces. 
 
a)   Are all 4 pieces equal-sized?  yes  /  no  /  don't know (Circle one)
 
 
 
 
 

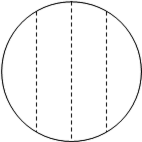
b)  Show how you would divide the circle into 4 equal-sized pieces.

 

Task administration: 
This task is completed with pencil and paper only.
Level:
2
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Keywords: 
fractions, partitioning
Description of task: 
Students identify whether two shapes have been partitioned evenly or not, and show how to correctly partition the shapes.
Curriculum Links: 
This resource can help to identify students' ability to find fractions of sets, shapes, and quantities.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Multiplicative thinking, sets 3-4
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
 
a)

 

i)
ii)

 

No and

or some other diagram with 3 equal-sized pieces.

1 mark
(for both i) & ii)
b)

 

 i)
ii)

 

No and

or some other diagram with 4 equal-sized pieces.

1 mark
(for both i) & ii)
Classroom-based research project about fractions, Y5 class, September 2005.

NOTE:  Students may be cued into suspecting the shown partitions are not even by phrasing of the question, but it is the way they partition the shape that is important.

Teaching and learning: 
The resource was developed to assess a common misconception about "even partitioning" of shapes that came out of classroom research into partitioning within fractions.  Partitioning is an important part of understanding the nature of fractions and the concept of evenness or equal sized partitions is fundamental to recognising the relationship between the part and the whole, and being able to name the part and combinations of the part.
Diagnostic and formative information: 
  Common error Likely misconception
a) Yes Students may have only experienced cutting up shapes that have rotational symmetry, so they apply this type of partitioning to all shapes indiscriminately.
b) Yes Partitioning the circle as strips.  Students' experience of partitioning may be limited to cutting things into strips.

 

Next steps: 
Some students have had limited experiences with fractions and partitioning and rely on the methods of cutting up they are familiar with.  If they have only ever divided up "pizzas" (or other shapes with rotational symmetry) they may think this is the only way to divide shapes up.  Using a cake which can be cut in many different ways or square pizzas can be used to challenge the students' concept of circular representations of fractions. Partitioning becomes more difficult when the partitions cannot be derived by a halving strategy, or the shapes are more complex and cannot easily be overlaid to check for equal-size.

It is also important to encourage students to explain how they know the partitions are even, and how they could justify this to somebody else (they may need to fold, or cut and overlay the pieces).

It is important that students build up many experiences of partitioning starting with…

  • halving of basic shapes, then halving multiple times to derive other parts;
  • partitioning a variety of shapes: squares, two squares, rectangles, circles, hexagons (which are easier to partition accurately than circles), etc.
  • partitioning shapes into a different number of pieces (e.g., 3, 5, 6, 7, 9, etc).

By partitioning shapes into odd numbered parts and with a range of shapes, students develop a more robust understanding of partitioning.  This variety ensures that they are not only remembering partitions with certain shapes, but that they are developing a strategy to represent and understand fractions and can partition any simple shape, recognising that these parts should be equal-sized.