Finding two-thirds
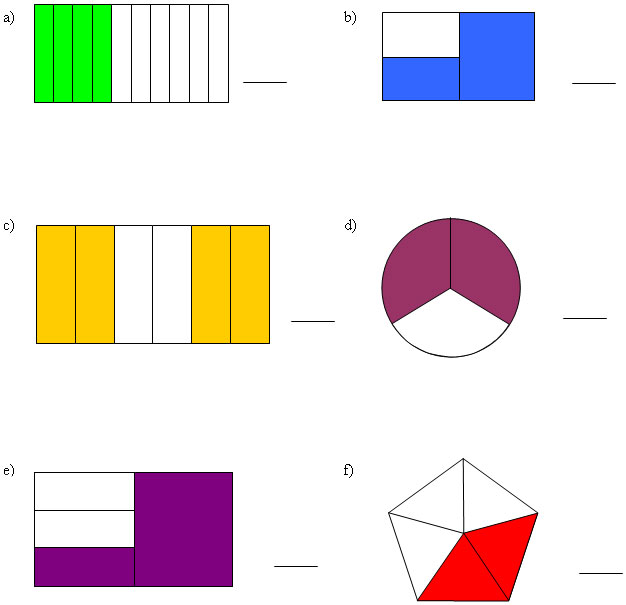
For the 8 shapes below:
- Write 23 next to all the shapes that are 23 shaded.
- If the shape is not 23 shaded, write what fraction of the shape has been shaded.
| Y6 (11/2007) | ||
| a) | 4/10 | very easy |
| b) | 3/4 | moderate |
| c) | 2/3 or 4/6 | very easy |
| d) | 2/3 | very easy |
| e) | 2/3 or 4/6 | moderate |
| f) | 2/5 | easy |
Students should already have had opportunity to explore partitioning to create fractions from regions and have some understanding that a fractional name represents a part-whole relationship between the bottom number (total number of equal-sized parts that make up the whole) and the top number (the number of these parts that make up the fraction).
About 40% of students made an error involving unequal sized pieces, i.e., working out the fraction shaded without taking into account the size of all the pieces.
| Common error | Likely misconception | |
|
b) e) |
2/3 (or 1/3) 2/4 |
Part-whole understanding of fractions – uneven size of pieces Students count the shaded pieces of each shape, and put that number over the total number of pieces, irrespective of the size of the piece (or combination of uneven pieces and finding the unshaded part.) |
|
a) b) c) d) e) f) |
6/10 or 3/5 1/4 2/6 or 1/3 1/3 2/6 or 1/3 3/5 |
Names the unshaded fraction Constructs the fraction for the unshaded part of the shape. |
|
a) b) c) d) e) f) |
4/6 2/1 4/2 or 2/4 2/1 2/2 2/3 |
Writing a fraction as a ratio of shaded to unshaded pieces Students count the number of shaded pieces and put over the number of unshaded pieces irrespective of the size of the pieces. If the answer is the inverse of these, then the student is comparing the unshaded to shaded pieces. |
Being able to recognise what fraction has been shaded involves being able to identify the total number of parts that the whole has been divided into and the number of these parts that are shaded (see Fractions as part-whole relationships). Students who construct the fraction by counting up the number of shaded pieces and putting that over the total number of pieces need to be aware when naming a fraction that each piece needs to be equal-sized. For example, when something is divided into quarters each of the 4 pieces has to be equal-sized. Encourage students to draw lines to create equal-sized partitions to help them work out or explain their strategy.
Asking the question "how much of the whole shape is shaded?" may also help eliminate this misconception.
Questions b), and f) involve parts that are not equal-sized. The idea of equal-sized parts is an important concept in the naming fractions
Possible exploration of the importance of equal sized parts
Get students to identify what fraction of a very simple shape is shaded,
"What fraction of the whole shape is shaded?

[Now draw a horizontal line across the shape.]
"What fraction of the whole shape is shaded now?
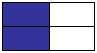
Show the same shape shaded in a different way
and ask "What fraction of the whole shape is shaded?"

Encourage students to recognise that the fraction of the whole shape that has been shaded is unchanged. Experiment by showing the same shape, but drawing lines to make smaller and larger pieces, each time asking "What if I draw a line here…what fraction of the whole shape is shaded?" e.g.,

Remind students that they are finding a part of a whole by asking "What is this part?" and "What is the whole?"
Students may also need to explore partitioning and to build up experience with constructing part-whole fractions. This should further encourage students to recognise the relationship between the bottom number (denominator) and the number of equal-sized pieces the shape is partitioned into (numerator).
Naming the unshaded fraction
Students who name the unshaded part may have simply made a reading error; however these errors may also be in conjunction with the misconception about equal-sized parts described previously.
Getting students to explain how they know what fraction the shaded part is should support them to self-correct their use of the unshaded parts. Exploring a range of different part-whole fractions should also get them used to finding the shaded part. Shaded fractions and Shaded Fractions II are two resources that look at part-whole fractions of regions.
Writing a fraction as a ratio of shaded to unshaded pieces
Students who construct the name of the fraction by merely counting up the number of shaded pieces and putting that number over the number of unshaded pieces are setting up the fraction as a ratio. Here the fraction is constructed by putting the number of shaded pieces on the top and the number of unshaded pieces on the bottom. A fraction compares a part to the whole, whereas a ratio compares a part to another part. Exploring Fractions as part-whole relationships should help students recognise how fractions are constructed.
NOTE: Ratios are a concept that students will need to develop, so it is important to affirm students' ideas in this area. The difference between a ratio and a fraction could be discussed and made explicit.
Book 7: Teaching Fractions, Decimals and Percentages, 2006:

