Partitioning sets
| a) |
i)
ii) iii) |
Show how to share the 15 counters equally between 3 people.
How many counters does each person get? _____ What fraction of the 15 counters does each person get? _____ |
 |
| b) |
i)
ii) iii) |
Show how to share the 35 counters equally between 5 people.
How many counters does each person get? _____ What fraction of the 35 counters does each person get? _____ |
 |
| c) |
i)
ii) iii) |
Show how to share the 24 counters equally between 8 people.
How many counters does each person get? _____ What fraction of the 24 counters does each person get? _____ |
 |
| d) |
i)
ii) iii) |
Show how to share the 54 counters equally between 6 people.
How many counters does each person get? _____ What fraction of the 54 counters does each person get? _____ |
 |
| Y6 (11/2007) | |||
| a) |
i) |
 or other acceptable partition into 6 equal-sized parts. 5 1/3 or 5/15 |
easy very easy |
| b) |
i) ii) iii) |
 or other acceptable partition into 5 equal-sized parts. 7 1/5 or 7/35 |
easy very easy |
| c) |
i) ii) iii) |
 or other acceptable partition into 8 equal-sized parts. 3 1/8 or 3/24 |
easy very easy |
| d) |
i) |
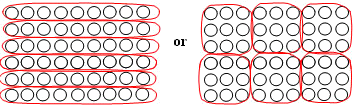 or other acceptable partition into 6 equal-sized parts. 9 1/6 or 9/54 |
easy
very easy |
NOTE: A number of students did not show how they could partition the sets. This showing of partitions is good scaffolding for exploring how to construct non unit fractions from the unit parts. However, partitioning also needs to be backed up by discussion about the fractional parts to ensure understanding.
Partitioning is an important understanding that lies at the heart of understanding fractions, percentages and decimals. It involves dividing an object or set of objects into a given number of equal-sized non-overlapping parts. Understanding that sets, shapes and amounts can be partitioned into equal parts is an important idea that helps understanding about the part-whole relationship between the numerator and denominator in fractions.
Most children who attempted to partition the shapes could indicate an equal partition. A small number of children partitioned the sets into a different number of parts (not into the number of part asked for). This is likely to depend upon the set and the number of people shared amongst. For example for question c) 24 counters shared amongst 8 people, a tenth of students simply partitioned the set into 4 or 6 parts. This does indicate the importance that students check their work by stating what part they have created by partitioning to confirm their understanding of the partition and how unit fraction can be created.
| Common error | Likely misconception | |
|
a) iii) b) iii) c) iii) d) iii) |
3 or 5 5 or 7 8 or 3 6 or 9 |
Cannot write fraction notation Students count the number of shaded pieces and write this as a whole number rather than a fraction. |
|
a) iii) b) iii) c) iii) d) iii) |
1/5 1/7 1/3 1/9 |
Fraction construction Constructing a fraction – using the number of counters each person gets and using this to create a unit fraction. Rather than recognising the part that each person would receive and putting that over the total). Not understanding which part is being sought, and what the referent whole is. |
|
a) iii) b) iii) c) iii) d) iii) |
3/15 5/35 8/24 6/54 |
Fraction construction Constructing a fraction with the number of partitions (not the number of counters that each person receives) over the total number of counters. Not understanding which part of the whole is being sought. |
|
a) iii) b) iii) c) iii) d) iii) |
3/5 (or 5/3) 5/7 (or 7/5) 8/3 (or 3/8) 6/9 (or 9/6) |
Part-whole misunderstanding of fractions Constructing a fraction by putting the number of people over how many counters in each person gets (or the number in each partition over the number of partitions). |
|
a) i) b) i) c) i) d) i) |
Not partitioning the set of counters amongst the given number of people. |
Not recognising the set as the whole being partitioned into n parts. Students partition the array into parts that suit the array rather than into the number of parts indicated. Students can be using geometric knowledge to answer the first part of the question without understanding the fractions there are creating. |
NOTE: Encourage students to use the word "fraction" rather than "part", as future fraction problems may ask for top heavy (or improper) fractions, e.g., 5 quarters, which is not so intuitively a "part".
Students who count the number of counters in a partition or the number of sets and write this as their answer may not recognise or know how to construct fractions, or they may have no understanding of the fraction as being a part of a whole and may need to further explore partitioning, and then fractions as part-whole relationships.
Not showing partitioning
Students who did not show how to partition the set, or partitioned it into another number of parts, need to be aware of the importance of partitioning in developing a more full understanding of fractions as parts of a whole. Partitioning can be a starting point to building up non-unit fractions. Encourage students to explain how they know the partitions are even for all the people they are shared amongst, and how they could justify this to somebody else (explaining, or using diagrams).
Part-whole misunderstanding of fractions – fraction construction
For students who can partition the set of counters into n parts, but not construct the fraction, ask them to name what fraction one part of the set is, reminding them that the whole is the whole set and the part is one of the partitions, e.g., "what fraction of the whole set is one of the groups?".
Partitioning is one way for students to explore constructing unit fractions. Focus discussion on building up understanding of what the part is and what the whole is for each maths problem they are working on. This encourages students to recognise that a fraction is a relationship between a part and a whole (part whole understanding of fractions). This whole can be a set, a region or a number.
The resource, Sharing counters (level 2), explores partitioning sets. This could be extended by asking the students to identify what fraction of the set one part is.
Equal sharing of sets, numbers or regions for simple problems and using a matching strategy is at Stage 4: Advanced counting - Stage 5: early additive part-whole. Students who can construct and name non-unit fractions are at Stage 5: early additive part-whole (using repeating addition) - Stage 6: Advanced additive (partitioning using division) part-whole.
Book 7: Teaching Fractions, Decimals and Percentages, 2006:
Animals, (p.7), Advanced counting/early additive part-whole.

