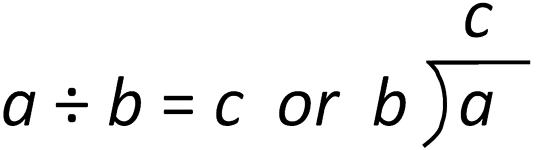How many groups? II

How many groups? II

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about finding the size and number of groups from a given total.
 
a)
 
 There are 36 pieces of chocolate to be shared equally. If each person gets 4 pieces of chocolate, show how to work out how many people the chocolate has been shared amongst.

 
 
 
 

How many people? _____
 
b)
There are 48 teddy bears altogether, and there are 8 teddy bears in each box. Show how to work out how many boxes of teddy bears there are. 

 
 
 
 

How many boxes? _____
 
c)
There are 56 Christmas trees. If 8 trees are sold to each shop, show how to work out how many shops get trees.

 
 
 
 

How many shops get trees? _____
 
d)
72 students are going to be taken to the zoo in vans. If there are 6 students in each van, show how to work out how many vans will be needed.

 
 
 
 

How many vans needed? _____
Task administration: 
This task is completed with pencil and paper only.
 
Level:
3
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Key Competencies: 
Using language, symbols, and texts
Keywords: 
division, quotition
Description of task: 
Students show how to divide given amounts into the number of groups of a given size.
Curriculum Links: 
This resource can help to identify students' ability to apply multiplicative strategies flexibly to whole numbers.
 
Links to the Number Framework
The strategies that students use can determine their stage of development within the Number Framework.  Strategies that could be used for this resource include counting out, one-to-one mapping, visual grouping, (partitioning and trial and error), repeated addition/subtraction, skip counting, multiplication, and division.  Students using repeated addition are indicating Stage 5 (Early additive) strategies, and students using multiplicative strategies are indicating Stage 6 (Early multiplicative).
Key competencies
This resource involves recording  strategies to perform division problems. This relates to the Key Competency: Using language, symbols and text.

Learning Progression Frameworks
This resource can provide evidence of learning associated with
Multiplicative thinking, sets 4-5
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
    Y6 (11/2006)
a) 9
Working that can involve:

  • Dividing the total by a factor: 36 ÷ ? = 4 [a small number of students wrote the equation in this form, most students wrote this as 36 ÷ 4 = ?];
  • Reverse multiplication: 4 × ? = 36;
  • Skip counting in 4's:  4, 8, 12, 16, 20, 24, 28, 32, 36 and counting how many 4's they used;
  • Repeated addition 4+4+4+4+4+4+4+4+4, and totalling;
  • Drawing an array (4 by 9);
  • Drawing a quotitive diagram: counting out four pieces for each person, then counting the number of groups (9);
  • Drawing a partitive diagram.
 easy
easy
b) 6
Working that involves any of the above strategies, i.e:.
Writing the problem as a division equation, reverse multiplication, skip counting, repeated addition, drawing a diagram (array, quotitive diagram, or  a partitive diagram).		 easy
easy
c) 7
Working that involves any of the above strategies.		 easy
easy
d) 12
Working that involves any of the above strategies.		 easy
easy

Based on a representative sample of 161 Year Y6 students.

Teaching and learning: 
These division problems are set out as "how many groups of x in this amount".  This type of division is known as quotitive division or quotition.  Division problems involving "equal sharing into x groups" is called partitive division or partitioning.
Diagnostic and formative information: 

Students strategies
60% of students used division or reverse multiplication strategies to solve these questions.  8% used an additive strategy (such as repeated addition or skip counting), and 6% used diagrams to solve the problems.  A very small number of students (2%) used a part-whole strategy to solve.  This was also a very successful strategy across all four questions.  The most consistent common successful strategy across all four questions was recognising the questions as a division and writing the equation in either form: 

division-layout-150h.png

Students who used this strategy averaged 90% success for the correct answer across all four questions.  Students who used reverse multiplication averaged 78% success with a wider variation.  Students who used repeated addition or skip counting averaged 54% success.

  Error Likely calculation Likely misconception
a)
b)
c)
d)		 4 ÷ 36 = 9
8 ÷ 48 = 9
8 ÷ 56 = 9
6 ÷ 72 = 9		   Students recognise that this is a division question but write the numbers as they might be written in long or short division format. (About 5% of students wrote the number sentence in this way).
a)
c)
d)		 144
64 or 48
78		 36 × 4
56 + 8 or 56 – 8
72 + 6		 Students use an incorrect operator (+, – , ×)
a)
b)
c)		 4
8
8		   Students may solve the problem but write down the same factor they have been given in the question.
a)
b)
c)
d)		 10/11
5 or 7/8
6 or 8
10/11		   Counting error – for additive strategies, e.g., repeated addition or skip counting.  The answer can be 1-2 counts away from the correct solution.
Next steps: 
For students who write the division in the incorrect order (i.e., 4 ÷ 36 = 9) ask them to read back the number sentence using the word "divided by" for division (as opposed to "goes into").  This error is a mathematical communication error rather than computational, as most of the students (93%) went on to get a correct answer. 
 
NOTE: Students may also be getting confused with the short and long division layouts.
 
For students who write the same factor they have been given in the question as the answer, it is likely they are getting the two factors confused.  Encourage them to devise a method to check their answer. For students who use an incorrect operator get them to draw or explain the story problem, e.g., "If each person gets 4 pieces of chocolate and there are 36 pieces, how could we show that?". Use simpler numbers as required, and encourage students to be able to justify their working. Get students to create their own story problems using all four operations to help them recognise how the operations sound in story problems, e.g., the resource Writing word problems for all operations or Making number sentences and Making number sentences (for multiplication and division) or use the keyword, story problems.
 
Students who use diagrams to show how to solve these questions should be encouraged to work towards visualising the problem and trying to solve it in their head.  This should encourage them to develop toward using known number properties.
 
A partitive diagram would be regarded as an incorrect representation of the relationship for these division questions.  
For example, for question a) a partitive diagram would look like 4 lots of 9 (36 being shared out into 4 groups):
4-groups-9.png
However these division questions ask how many groups if there are 4 in a group. 
This would look like 9 lots of 4 (with 9 being the unknown):
9-groups-4.png
 
Why quotition?
The distinction between quotitive and partitive division becomes important when students are asked questions like 2 ÷ 1/2.  If they only have experience with the equal sharing model of division they will try to equally share 2 between a half (which may not make much sense to them), whereas if they could say "how many 1/2s in 2?" the problem becomes considerably more accessible.  Accordingly it is important to give students a range of experiences with these different aspects of division to develop a more full understanding of division, including the relationship between division, addition, and multiplication (multiplicative inverse).
 
Extension:
After students have finished the questions have them engage in whole class discourse through sharing the strategy they used to solve the problem and then identifying the most efficient strategies.