Number line addition and subtraction II
 |
|
Example: Sarah had to solve this problem: 96 –  = 64. = 64.She knew that 96 – 30 = 66, and that 66 – 2 = 64. So she showed this on the number line and then wrote the answer in the box: 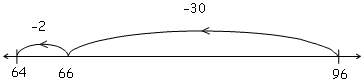 96 – 96 –  = 64 = 64 |
Use the number lines below to show how to solve the equations.
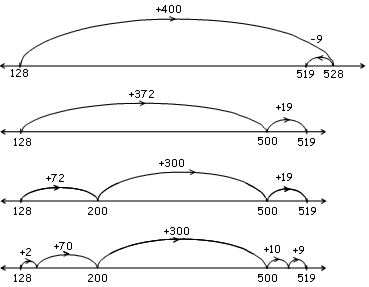
a) 128 +  = 519
= 519 
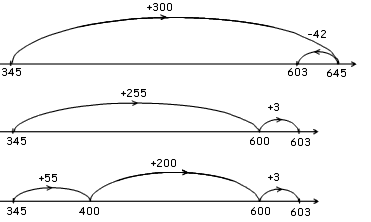
b) 345 +  = 603
= 603 
c) 530 –  = 327
= 327 
d) 906 –  = 625
= 625 
| Y8 (06/2006) | ||
| a) |
391 |
moderate |
| b) |
258 |
moderate easy |
| c) |
203 The number line is used to show jumps added/subtracted that use the sequential nature of the number line, e.g., 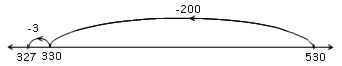 or other acceptable jumps that represent the equation. NOTE: Also accept a "reversed" number line as a suitable representation of the equation, but encourage students to use the convention of a number line incrementing left to right.] 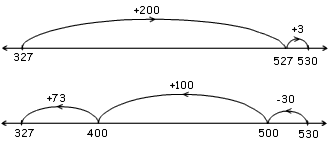 Complementary addition 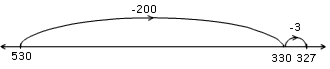 |
moderate easy |
| d) |
281 The number line is used to show jumps added/subtracted that use the sequential nature of the number line, e.g., 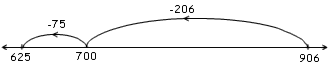 Complementary addition 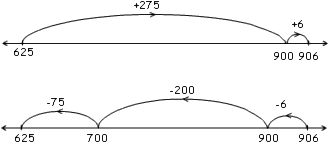 or other acceptable jumps that represent the equation. NOTE: Also accept a "reversed" number line as a suitable representation of the equation, but encourage students to use the convention of a number line incrementing left to right.] 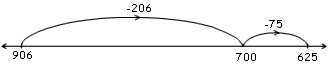 |
difficult moderate |
For the subtraction problems a number of students set up the number line beginning with the higher number on the left and jumping to the lower number on the right. While this is not how number lines are conventionally set up, this is still “showing how to subtract on a number line”. This common strategy could be a step toward recognising the complementary nature of addition and subtraction, and students could be further supported by being asked how they could show these jumps if the number line was increasing (i.e., either subtracting by jumping back or adding by jumping forward from the smaller number).
Over half of students solved the equations by either using place value partitioning (grouped by place value, i.e., + 30 not + 10 + 10 + 10), jumping to and from tidy numbers or recognising compatible numbers and jumping to numbers that related to the target number on the number line.

Without the size of the jumps indicated there is no evidence that the number line is actually being used to represent or solve the equation (although they have solved the equation using some other strategy).
As this resource is about representing operations on a number line, students who responded like this may need to look at how or why it can be useful (e.g., being able to identify and show a range of strategies, and compare for efficiency) to show addition and subtraction as jumps on a number line. If required, get students to use basic addition problems such as those found in Number line addition. Using the examples given, ask questions like "What happens if I start here and add 10?", or "How do we show the addition on the number line?" Encourage students to represent an approximate jump – not count out and draw in marks, but just draw. Mark the size and direction of the jump, and the new location on the number line.
For students who can show basic place value jumps on the number line, encourage them to use fewer jumps to solve the equation more efficiently and reflect on which strategies best suit the particular equation. This may involve using tidy numbers or compatible numbers rather than jumps made strictly by place value partitioning, and may also involve jumping past the target number, then back to it.
For students who solved the equation using the vertical algorithm and then represented the answer on the number line, encourage them to use jumps on the number line as a tool to solve and reflect on the jumps that could make this most efficient (as above).
Showing how to solve addition problems on a number line can require jumping to tidy numbers, or using tidy numbers to make the jumps, and then making an adjustment to complete the equation. Students can also use elements from place value partitioning, or compatible numbers, to jump along the number line. Number lines can provide a way for students to image addition or subtraction as forward or backward jumps.
A simple place value partitioning strategy with unitised jumps – not grouped (i.e., + 10 + 10 + 10 + 10 instead of + 40) – may indicate an early additive part-whole understanding. To indicate advanced additive part-whole thinking, students would use fewer jumps (more efficient jumps) to solve equations and be able to use or identify different ways to show how to solve the equation (multiple strategies).
- Maths Detective (Number sense and Algebraic thinking, L3, book 2, pages 2-4), and
- Tidying up (Number sense and Algebraic thinking, L3, book 1, pages 2-4).