What are basic facts?
When we think of basic facts, possibly the first thing that springs to mind are our “times tables”. But there is far more to them than this. We should memorise simpler facts, like our addition and subtraction facts. Often these have been ignored. Just maybe 7 × 8 may pop into mind just a tad more automatically than 7 + 8.
Main points about basic facts
Just about anything in mathematics can be a basic fact. The main ones encountered are the whole-number basic facts, and in particular addition and multiplication, and their close cousins subtraction and division.
We also suggest including a growing number of instantly recognisable or retrievable facts into basic mathematical factual knowledge (basic facts). For example, it is highly useful to instantly equate the fact that ½, 0.5, and 50% are alternative representations of the same amount.
As we advance in mathematics we acquire whole bodies of other basic facts such as “The sum of the angles in a triangle equals 180º”, Pythagoras’ Theorem, or many other things. Every time we meet one of these we don’t try and prove it all over again. We just bring it out of our memory to help solve a problem, or to use as one step in a more complex line of reasoning. If we didn’t do this, we would have to start right back at square one for everything we wanted to do in mathematics.
A definition of basic facts
|
"Any number or mathematical fact or idea that can be instantly recalled without having to resort to a strategy to derive it." |
Basic facts covered in this concept map
- Traditional basic facts (on whole numbers)
- Addition up to 10 + 9, and subtraction up to 19 – 9
- Multiplication up to 10 × 10, and division up to 100 ÷ 10
Related basic facts (on whole numbers)
- Addition and subtraction related to the traditional basic facts e.g. 40 + 50, 130 – 60
- Multiplication and division related to the traditional basic facts e.g. 40 × 5, 280 ÷ 40
- Other useful basic facts (on whole numbers)
- Other multiplication tables e.g. 100×, ×1000× etc: 25×, 125×, 11.1×
- Factors and multiples
- Whole number patterns
- Basic facts for fractions, decimals, and percentages
Why is it important to learn the basic facts?
To free the brain up for other aspects of the mathematics we are involved with. Scientists have discovered that there is only so much the brain can keep in its short-term working memory. Having a vocabulary of "facts" allows a student's short-term memory to devote its attention to other less obvious aspects of a mathematics problem, or suggest a possible method of attacking the problem. Memorised facts are stored in a different part of the brain than those that are used for performing strategies (Sousa, 2008). Separate activities are needed to explore and practice strategies than those which are used to build up and to reinforce memorisation of the basic facts.
Basic facts should be automatic and random
Automatic basic facts
While strategies are important, students need to progress to the point where they the automatically recall the basic facts while they focus their full attention to other aspects of the mathematics. Having to revert to even the simplest of strategies takes up valuable brain processing room.
Random basic facts
Students need to randomly access their basic facts rather than recover them sequentially. This is especially so for multiplication, where students need instant access to 7 × 4 without having to recite the 4-times table starting from 1 × 4 = 4, 2 × 4 = 8, etc. This means that rote learning has only a limited role to play, and other memorisation techniques need to also be adopted.
- Addition is the joining together of two sets.
- Counting on is the fundamental idea of addition.
- Addition basic facts encompass the traditional addition facts up to 10 + 9
- These are the first basic facts learnt. We should emphasise addition facts earlier than the multiplication facts, but often these have not been memorised so rigorously as the multiplication facts.
The following principles apply to addition facts:
- The smaller both numbers are, the quicker children learn these facts and the faster they recall the facts.
- Children learn and recall doubles easily (2 + 2, 9 + 9, etc.) regardless of the size of the numbers.
- Adding on 0 and 1 is very easy. These are so self-evident that we probably won’t need students directly need to memorise them. However, it is useful for students to be aware of them, recognise them, and know how to use them. Add on from the larger number is generally more efficient. See the striped parts of Tables 1-3.
-
Addition is commutative, so some basic facts up can be derived from known ones,
e.g., 2 + 3 = 3 + 2
Strategies that underpin basic addition facts are developed and memorised as follows:
- Facts to 5: Counting strategies (plus doubles to 10) see Table 1
- Facts to 10: Counting strategies (plus doubles to 10) see Table 2
- Facts 11 to 18: Counting strategies (see Table 3)
- Facts to 18: Using derived facts (see Tables 4)
- Addition strategies and basic facts
- Extending addition number facts
This is gives a rough guide to the order that the addition facts will be learnt–remember that initially strategies need to be explored. After this, separate activities need to be done to build and reinforce memorisation.
A) Facts to 5 – Counting strategies
Table 1 - Counting strategies for addition basic facts up to 5
Second number
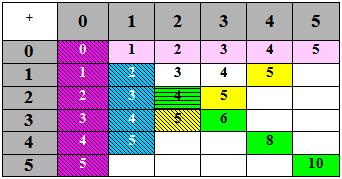
Students are likely to memorise facts in roughly the following order:
| Purple | Adding nothing – this leaves the number unchanged |
| Blue | Adding one gives the next number in counting sequence |
| Green | Doubles to 5 (and also to 10). Students often know them to 10 – see the unstriped ones. |
| Yellow | Groupings within 5 |
Points
- The striped facts use the most efficient “count on from the larger number”
-
The non-coloured facts in the upper triangle require the less efficient method of counting on from the smaller number.
They can be obtained from the striped facts as derived facts using commutativity (e.g. 2 + 3 = 3 + 2)
B) Facts to 10 – Counting strategies
Table 2 - Counting strategies and addition basic facts to 10
Second Number

The facts are likely to be memorised in roughly the following order:
| Purple |
Adding nothing leaves the number unchanged or 0 + a number = that number (the unstriped light purple) or 10 + 6 = 16, 10 + 8 = 18 (the unstriped light purple) |
| Blue |
Adding one gives the next number in counting sequence. The facts such as 1 + 4 are not counting on by 1, but use commutativity to get 4 + 1 |
| Green | Doubles to 10 (and to 18) |
| Yellow |
Groupings within 10 (the unstriped ones are often known, but require counting on from the smaller number) |
| Red |
Groupings within 10 (the unstriped ones are often known, but require counting on from the smaller number) |
Points
- The non-coloured facts in the upper triangle can be got from the striped facts using commutativity (e.g., 4 + 5 = 5 + 4, which is a derived fact).
- Students are likely to be able to recall the dark red facts of Table 2 last.
C) Facts 11 – 18: counting strategies
Students may continue with counting strategies, but need to progress onto facts derived from known basic facts using part-whole strategies.
Table 3 - Counting strategies and addition basic facts to 1
Second Number
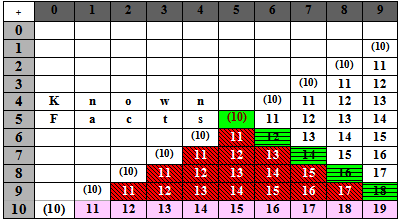
The facts are likely to be memorised in the roughly the following order:
| Light Purple | Ten plus a number |
| Green |
Doubles to 18 – This is given horizontal stripe because it is the mirror line of all tables. |
| Red | Count on from the bigger number to 18 |
Points
- The non-coloured facts in the right-hand triangle can be got from the red facts using commutativity (e.g., 4 + 8 = 8 + 4).
- Students are likely to be able to recall the dark red facts of Tables 2 and 3 last.
D) Facts to 18: using derived facts
Table 4 - Derived addition basic facts to 18
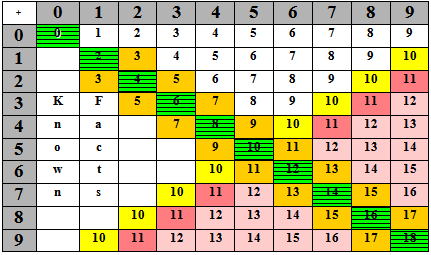
The facts are likely to be memorised in order by the colours:
| Green | Doubles to 10 or 18 (Already known) |
| Yellow |
Groupings within 10 (Already known) |
| Orange | Near doubles (derived facts) |
| Pink |
Near groupings to 10 (derived facts), e.g., 7 + 4 = 11 because 7 + 3 + 10 so its 1 more |
| Light pink |
Grouping to 10 and then use groupings to 10 and compensation, e.g. 8 + 5 = 13 because 8 + 2 = 10 and 10 + 3 = 13 |
| No colour |
Commutativity from known facts |
Point
Commutativity can be used on all the regions of Table 4 above the green diagonal line (the doubles to 18).
E) Addition strategies and basic facts
The range of specific strategies is listed in order of increasing sophistication in Table 5. The Number Framework strategy stage is indicated in brackets, and the order that the facts are likely to be learnt is also indicated, though this can differ for individual learners. While these comments apply to addition and counting on, the effect of counting back and counting up for subtraction can also be explored simultaneously.
|
Helpful strategies |
Stage |
Example: |
|
Count all the objects |
2 |
2 + 3: 1, 2, 3, 4, 5 |
|
Count on by 1 Blue |
2-3 |
4 + 1: 1 more than four is 5 |
|
Count on by 0 Purple |
4 |
4 + 0: This is just 4. It is the same as 0 + 4 |
|
Explore doubles Green |
3-4 |
3 + 3: 3, 4, 5, 6 |
|
Make to 5 or 10 Yellow |
4 |
6 + 4: exactly equal 10 |
|
Count on Red from the larger number |
4 |
2 + 3: 2, 3, 4, 5 and 3 + 2: 3, 4, 5 |
|
Near doubles Orange |
5 |
3 + 4: I know 3 + 3 = 6 so it is 6 + 1 = 7 |
|
Ten-plus facts Light Purple |
4 |
10 + 7: This is 17 (place value knowledge, or skip count by 10) |
|
Commutativity |
|
2 + 7: I know 7 + 2 = 9, so 2 + 7 = 9 |
|
Part-whole partitioning Light pink |
|
8 + 5: 8 + 2 = 10; 10 + 3 = 13 (as 2+3=5) |
F) Extending addition basic facts
Place value knowledge allows a rich range of strategies to build on the basic addition facts. Several of these follow, and many mixtures of them are also possible. Multiples of 10, 100, etc. The basic addition facts to 18 apply to single digit numbers only. These can be extended to multi-digit numbers as shown below:
| Basic facts to 9: | |
|
30 + 20 = 50, 400 + 500 = 900, 0.3 + 0.5 = 0.8, |
because 3 + 2 = 5, so the answer is 5 tens = 50 because 4 + 5 = 9, so the answer is 9 hundreds = 900 because 3 + 5 = 8, so the answer is 8 tenths = 0.8 |
|
Groupings within 10 |
|
|
30 + 70 = 100, 800 + 200 = 1000, 0.6 + 0.8 = 1.4, |
because 3 + 7 = 10, so the answer is 10 tens = 100 because 8 + 2 = 10, so the answer is 10 hundreds = 1000 because 3 + 7 = 10 |
|
Basic facts to 18: |
|
|
40 + 90 = 130, 700 + 500 = 1200, 0.6 + 0.8 = 1.4, |
because 4 + 9 = 13, so the answer is 13 tens = 130 because 7 + 5 = 12, so the answer is 12 hundreds = 1200 because 6 + 8 = 14 |
Some students may automatically recall more complex facts such as:
46 + 8 = 54 because 6 + 8 = 14
457 + 4 = 461 because 7 + 4 = 11
37 + 23 = 60 because 7 + 3 = 10 and 30 + 20 + 10 = 60
41 + 59 = 100 because 1 + 9 = 10 and 40 + 50 + 10 = 100
570 + 60 = 630 because 7 + 6 = 13, so 70 + 60 = 130 and 500 + 130 = 630
3400 + 900 = 4300 because 4 + 9 = 13, so 400 + 900 = 1300 and 3000 + 1300 = 4300
300 + 50 + 7 = 357 [Place value decomposition]
Resources
- Subtraction basic facts encompass the traditional facts up to 19 - 9
- Subtraction is taking a (smaller) set away from another (larger) one.
- Counting back is the fundamental idea of subtraction.
- Subtraction is closely linked to the addition basic facts, but students find them harder to memorise.
- Subtracting 0 or 1 is very easy (see the purple and blue parts of Table 5).
- Subtracting two single digit numbers is easy (see top half of Table 5).
- Subtraction involving doubles is easy (see the green parts of Table 5).
- Subtraction is not commutative (7 – 2 ≠ 2 – 7)
- Subtraction may lead to negative numbers.
Table 6 - Counting strategies and subtraction basic facts to19
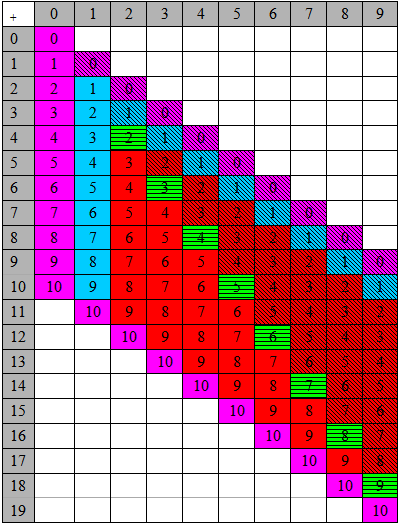
Facts are in approximate order of difficulty are listed below:
| Purple |
Taking off 0 leaves a number the same (purple and unstriped) or A number minus itself = 0 (purple and striped) or 19 – 9 = 10; 16 – 6 = 10 (purple and unstriped) |
| Blue |
Taking off 1 |
| Green |
Doubles or halves e.g. 8 – 4 = 4 becausehalf of 8 is 4, 8 – 4 = 4 because4 + 4 = 8 |
| Red |
Count back from … by … e.g. for 9 – 2 count back from 9 by 2, i.e. 9, 8, 7 |
| Red |
Count back from … until … e.g. for 8 – 6 count back from 8 until reach 6; i.e. 8,1 7,2 6 |
|
Count on from … until … e.g. for 8 – 6 count on from 6 until reach 8; i.e. 6,1 7,2 8 |
Derived subtraction facts
If some addition facts are known, then other subtraction facts can be derived from them using Families of facts (Stage 4). Students can use their knowledge of addition facts to derive and quickly recall subtraction facts. Each addition fact has two related subtraction facts. This is much easier for single digit minus single digit subtraction. These can all be understood by the number properties of the additive inverse and of the additive identity. Examples:
Knowing that 5 + 3 = 8 helps with 8 – 3 and 8 – 5
Knowing that 8 + 6 = 14 helps with 14 – 6 and 14 – 8
8 – 4 = 4 because 4 + 4 = 8 (halving is related to doubling)
10 – 3 = 7 and 10 - 7 = 3 because 3 + 7 = 10 (groupings to 10)
Extending the subtraction facts
This is broadly the same as extending the addition facts
Multiples of 10, 100, etc.
The basic subtraction facts to 18 can be extended to multi-digit numbers.
|
Basic facts to 9: |
|
|
17 – 13 = 3, |
because 7 – 3 = 4 |
|
90 – 20 = 70, |
because 9 – 2 = 7, so the answer is 7 tens = 70 |
|
500 – 300 = 200, |
because 5 – 3 = 2, so the answer is 2 hundreds = 200 |
|
0.8 – 0.5 = 0.3, |
because 8 – 5 = 3, so the answer is 3 tenths = 0.3 |
|
Groupings within 10 |
|
|
170 – 70 = 100, |
because 17 – 7 = 10 so the answer is 10 tens = 100 |
|
1200 – 200 = 1000, |
because 12 – 2 = 10 so the answer is 10 hundreds = 1000 |
|
630 + 30 = 600, |
because 63 – 3 = 60 |
|
Basic facts to 18: |
|
|
130 – 90 = 40, |
because 13 – 9 = 4 so the answer is 4 tens = 40 |
|
1300 – 500 = 800, |
because 13 – 5 = 8 so the answer is 8 hundreds = 800 |
|
1.6 – 0.9 = 0.7, |
because 16 – 9 = 7 |
Resources
- Multiplication is joining together several sets of the same size.
-
Repeated addition is a fundamental model for multiplication,
e.g., 3 × 6 = (2 × 6) + 6 = [(1 × 6) + 6] + 6 = 6 + 6+ 6 - Multiplication includes the facts to 10 × 10.
- Students can also be exploring division strategies, and learning division basic facts at the same time as learning about multiplication.
- We will use the convention that 4 × 7 is the same as 4 lots of 7. This means that the 4-times table is column 4 of Tables 7 and 8.
The following principles apply to multiplication facts:
- Multiplying by 0 or by 1 is very easy. These are so self-evident that we probably won’t need students directly need to memorise them. However, it is useful for students to be aware of them and know how to use them.
- Some times tables are easier to learn than others
- Multiplication is commutative, so some basic facts can be derived from known ones e.g. 5 × 8 = 8 × 5
A most likely order to memorise the tables is:
-
1- and 10-times table because adding on 1 is very easy, as is adding on 10 if the students understand place value.
2-times table because adding on 2 is very simple
5-times table which is just the intermediate jumps of the 10-times table. - 3-times and 4-times tables. Adding on small amounts is easier than large amounts.
- 6- to 9-times tables.These can be approached by repeated addition, but it is increasingly difficult to do this using addition alone without exploiting derived facts or patterns. It is useful for students to derive each table using repeated addition.
A) 1-, 10-, 2-, and 5- times table
1-times table: Purple
This is just the counting numbers; 1, 2, 3, 4, …, 9.
10-times table: Blue
The sequence 10, 20, 30, 40, is jumps (repeated addition) of 10 rather than 1.
2-times table: Blue
It can easily be obtained from repeated addition of 2.
It is just the sequence of doubles. Students often know this from their addition knowledge (plus commutativity). e.g. 4 × 2 = 2 × 4 = 4 + 4 = 8
5-times table: Blue
This follows from the 10-times table, just filling in the jumps half way between the successive 10s.
Table 7 - 1, 2, 5, and 10 times tables
Second Number
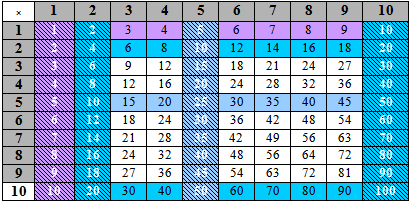
Points
- This gives 40 basic facts (the striped regions). The 2-times table is the second column.
- Commutativity gives another 24 basic facts. (unstriped coloured region), e.g. 5 × 7 = 7 × 5 = 35
B) 4-, and 3- times table
4-times table: Green
This can be by doubling a known times table (the 2× table). Almost all the doubles are already known or are easy, except 8 × 4 = 2 × 16 = 32 and 9 × 4 = 2 × 18 = 36
It can also easily be obtained from repeated addition of 4.
3-times table: Green
This can easily be obtained from repeated addition of 3. It can also be derived from the 2-times table e.g. 6 × 3 = 6 × 2 + 6 = 18 This is equivalent to working across the rows of Table 7.
Table 8 - 3- and 4-times tables
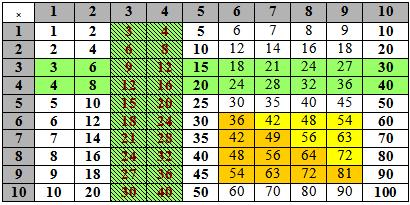
Points
- This gives another 12 new basic facts: 3 × 3, 4 × 3, 6 × 3, …, 9 × 3; and 3 × 4, 4 × 4, 6 × 4, …, 9 × 4
- Commutativity gives another 8 basic facts.
C) 6- to the 9- times tables
There are only 16 basic facts to complete the 6- to the 9- times tables. These are the ones in Orange or Yellow . Of these facts, the six Yellow basic facts can be obtained using commutativity, i.e. 7 × 8 = 8 × 7. Strategies that underpin basic multiplication facts are as follows:
| 1. | Counting on from 1 | (Stages 2 - 3) | use for 2×, 3× and 4×, e.g., 4 × 2 = 1, 2, 3, 4, 5, 6, 7, 8 |
| 2. | Skip counting | (Stage 4) | use for 2×, 10×, 5×, e.g., 4 × 2 = 2, 4, 6, 8 |
| 3. | Repeated addition | (Stage 5) | use for 2×, 3× and 4× (5×), e.g., 4 × 2 = 2 + 2 + 2 + 2 |
| 4. | Commutativity | 5 × 7= 7 × 5= 35 (know 5× table) | |
| 5. | Derived facts | (Stage 6+) | use for 3×, 4×, 6×, 8× and 9× |
| 6. | Patterns | (Stage ?) | use for 2×, 4×, 6×, 8× and 9× |
Patterns in multiplication
Exploring patterns in the times tables is another useful approach that both gives interest to, and aids the memorisation of the times tables. Every table has a repeating pattern of some sort, even the least accessible of all, the 7-times table. Intriguing links can be seen between the last digits in the times table. See Table 9, which shows how the last digit in each pair of times tables is the exact reverse of each other. It looks as if this is a feature of having a base–10 number system, and this then explains the commonly known pattern of the 9-times table.
Table 9 - Patterns in the ones digit of the times tables
|
Table |
Last digit |
Table |
Last digit |
|
1× |
1 2 3 4 5 6 7 8 9 |
9× |
9 8 7 6 5 4 3 2 1 |
|
2× |
2 4 6 8 0 2 4 6 8 |
8× |
8 6 4 2 0 8 6 4 2 |
|
3× |
3 6 9 2 5 8 1 4 7 |
7× |
7 4 1 8 5 2 9 6 3 |
|
4× |
4 8 2 6 0 4 8 2 6 |
6× |
6 2 8 4 0 6 2 8 4 |
The nine-times table pattern
This pattern is very well known, and is found in many disguises.
The ones digit starts at 9 and goes down by 1 (9, 8, 7, …)
The tens digit starts at 0 and goes up by 1 (0, 1, 2, …),i.e. the digit in the tens place is one less than the number of times 9 is being multiplied.
The digit in the ones place plus the digit in the 10’s place = 9
6 × 9 = 54 because 5 is 1 less than 6, and 5 + 4 = 9
1 × 9 = 9
2 × 9 = 18
3 × 9 = 27
4 × 9 = 36 etc.
Repeating patterns in multiplication
In many of the tables, the digits cycle in useful ways. The ones digits have various “cycle lengths” before they repeat. Once the ones digit completes or begins a new cycle, it is a signal that something may also happen to the tens digit.
Cycle length 1: 10-times table
The ones digit is always 0, the tens digit goes up by one
Cycle length 2: 5-times table:
Tens digit goes: 0, 1, 1, 2, 2, 3, 3, 4, 4, 5
Ones digit goes: 5, 0, 5, 0, 5, 0, 5, 0, 5, 0
Cycle length 5: The 2-, 4-, 6- and 8- times tables
These repeat the ones digits in a cycle of 5. This means that if you know the table up to 5, the table up to 10 is easy. It is especially memorable for the 2- and the 8-times table.
2-times table:
Tens digit goes: 0, 0, 0, 0, 1, 1, 1, 1, 1, 2
Ones digit goes: 2, 4, 6, 8, 0, 2, 4, 6, 8, 08-times table:
Tens digit goes: 0, 1, 2, 3, 4, 4, 5, 6, 7, 8
Ones digit goes: 8, 6, 4, 2, 0, 8, 6, 4, 2, 0
The 4- and the 6- times tables also have repeating patterns in the ones digit based on the even digits.
For the 4-times table the ones digit cycle is: 4, 8, 2, 6, 0
For the 6-times table the ones digit cycle is: 6, 2, 8, 4, 0, which is just the reverse of the 4- times table.
Cycle length 10: 3-, 7-, and 9-times table (plus the 1-times table)
9-times table:
Tens digit goes: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Ones digit goes: 9, 8, 7, 6, 5, 4, 3, 2, 1, 0
There is, however, a pattern for the 3- and the previously intractable 7-times table.
3-times table:
Tens digit goes: 0, 0, 0, 1, 1, 1, 2, 2, 2, 3
Ones digit goes: 3, 6, 9, 2, 5, 8, 1, 4, 7, 07-times table:
Tens digit goes: 0, 1, 2, 2, 3, 4, 4, 5, 6, 7
Ones digit goes: 7, 4, 1, 8, 5, 2, 9, 6, 3, 0
Just look, in both cases the tens digit does something interesting at the end of each sub-cycle of 3! The pattern in the ones digit is the exact reverse in the 7-times tables as it was for the 3-times table.
Extending the multiplication basic facts
The extended 10-times table
Any number multiplied by ten is just that number with a 0 on the end. This is because our number system has a base of 10.
Example:
26 × 10 = 260, or equivalently 340 is 34 lots of 10.
We can then extend the basic facts as follows:
60 × 4 = 240 because it equals (6 × 4) × 10 = 24 × 10 = 240
The hyper-extended 10-times table
Students should know the effect of multiplying different powers of ten together. Again this is just the result of our base-10 number system. The first few of these are summarised in Table 10.
Example:
100 × 10 000 = 1 000 000
This is because 100 = 10 × 10 and 10 000 = 10 × 10 × 10 × 10
So 100 × 10 000 = 10 × 10 × 10 × 10 × 10 × 10 = 1 000 000 = 106
(Which is a 6-dimensional hyper cube!)
We can then extend the basic facts as follows:
60 × 400 = 24 000, because it equals (6 × 4) × 10 × 100 = 24 × 1000= 24 000
4000 × 50 = 240, because it equals (4 × 5) × 1000 × 10 = 20 × 10 000 = 200 000
Table 10 - The hyper-extended ten-times table
|
× |
10 |
100 |
1000 |
10 000 |
100 000 |
|
10 |
100 |
1000 |
10 000 |
100 000 |
1 000 000 |
|
100 |
1000 |
10 000 |
100 000 |
1 000 000 |
10 000 000 |
|
1000 |
10 000 |
100 000 |
1 000 000 |
10 000 000 |
100 000 000 |
|
10 000 |
100 000 |
1 000 000 |
10 000 000 |
100 000 000 |
1 000 000 000 |
|
100 000 |
1 000 000 |
10 000 000 |
100 000 000 |
1 000 000 000 |
10 000 000 000 |
Doubling and halving
This is particularly useful once the hard-to-learn facts are known (i.e. where both numbers are between 6 and 9). This leads to the following:
-
12-times table (from 1 to 5)
6 × 2 = 12 = 12 × 1,
6 × 4 = 24 = 12 × 2,
6 × 6 = 36 = 12 × 3,
6 × 8 = 48 = 12 × 4,
6 × 10 = 60 = 12 × 5
- The 14-, 16-, 18-, and 20-times tables can similarly be derived, e.g. 9 × 8 = 72 = 18 × 4.
Other useful multiplication tables
11-times table and the 11.1-times table
The ones digit and the tens digit are the same. So the sequence goes:
1 × 11 = 11, 1 × 11.1 = 11.1,
2 × 11 = 22, 2 × 11.1 = 22.2,
3 × 11 = 33, 3 × 11.1 = 33.3,
…,
9 × 11 = 99, 9 × 11.1 = 99.9 = 100
and 10 × 11 = 110 (using the extended 10-times table)
25-times table
All that we need to know is the following:
1 × 25 = 25 (which is obvious)
2 × 25 = 50 (which many people seen to know as a doubles fact)
3 × 25 = 75 (which is just 25 more than 50 and is often known)
4 × 25 = 100 (which is often known, or is double 50)
Then we get the repeating pattern:
25, 50, 75, 100
125, 150, 175, 200,
225, 250, 275, 300, … where each hundred is 4 lots of 25.
The 5-times table can help us because 25 × 2 = 50 and
The 4-times table can also help because 25 × 4 = 100,
125-times table
All that we need to know is the following, with the bolded ones the only new ones once the 25-times table is known:
1 × 125 = 125 (which is obvious)
2 × 125 = 250
3 × 125 = 375
4 × 125 = 500 (which is double 250 from the 25-times table)
5 × 125 = 625
6 × 125 = 750 (which is triple 250 from the 25-times table)
7 × 125 = 875
8 × 125 = 1000 (which is quadruple 250 from the 25-times table)
15-times table
This is related to the 3-times table because 15 × 2 = 30 and this can be seen in following patterns:
15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, …
35-times table
This is related to the 7-times table because 35 × 2 = 70 and this can be seen in following patterns:
35, 70, 105, 140, 175, 210, 245, 280, 315, 350, 385, 420 …
45-times table
This is related to the 9-times table because 45 × 2 = 90 and this can be seen in following patterns:
45, 90, 135, 180, 225, 270, 315, 360, 405, 450, 495, 540 …
This is particularly useful for angles in Geometry.
Resources
- This includes the facts to 100 ÷ 10.
- Division can be thought of as either:
- finding the size of a set when objects are shared equally (partitive division); or
- finding the number of sets when objects are shared equally (quotitive division).
- Repeated subtraction is the fundamental idea of division.
- Division is closely linked to the multiplication basic facts.
The following principles apply to division facts:
- Dividing by 1 is very easy. This is so self-evident that we probably won’t need students directly need to memorise them. However, it is useful for students to be aware of them, recognise them, and know how to use them.
- Dividing by 0 has no meaning.
- Division is not commutative (8 ÷ 2 ≠ 2 ÷ 8)
- Division often leads to fractional (rational) numbers, e.g. 5 ÷ 3 = 5/3 = 1.6.
Reverse multiplication
The major strategy for division is recognising that it is the inverse of multiplication (the multiplicative inverse). This means that basic division can be related to an associated multiplication basic fact. Example: 7 × 5 = 35 means that 35 ÷ 7 = 5 and 35 ÷ 5 = 7
Divisibility
There are easy rules which indicate if any whole number is exactly divisible by a given amount. While these are not basic division facts, they are useful to know. This table gives the rules in a probable order of acquisition. This roughly corresponds to order that the multiplication tables are learnt. This allows students to have an increased vocabulary of numbers which they can instantly recognise the factors of.
Table 11 - Divisibility rules
|
Divisor |
Divisibility rule |
Example |
|
2 |
The last digit is even (0, 2, 4, 6, 8) |
3578 |
|
10 |
The last digit is 0 |
1 236 760 |
|
5 |
The last digit is 0 or 5 |
1 236 675 |
|
3 |
The sum of the digits is divisible by 3. |
468 as 4 + 6 + 8 = 18 |
|
9 |
The sum of the digits is divisible by 9. |
3258 |
|
6 |
The number is divisible by 2 and 3 |
348 |
|
4 |
The last two digits are divisible by 4. |
3136 |
|
Strategise – Practice – Memorise |
Understanding and strategies are the most important aspects of mathematics, but this does not exclude the role of memorisation. Each one helps the other.
- Start with strategies
- Plenty of practice
- Move on to memorise the basic facts
1) Start with strategies
Research has shown that it is inefficient to try and remember facts which do not have a firm meaning to the student. There is little point trying to get a student to learn their times-tables if they have no understanding of multiplication.
Students should also have a strategy, or preferably a range of strategies that they understand and can use to obtain the result that we want them to eventually memorise.
Basic facts should not just be rote-learnt in isolation from understanding. There is little point knowing what 6 + 7 or 7 × 8 is, if the student has no concept of addition or of multiplication. Teaching needs the joint foci on developing understanding as well as memory.
2) Plenty of practice
Doing a wide variety of work that aims to build and enhance strategies, helps reinforce procedures, and understanding of mathematics. Practising strategies also reinforces and continues the process of memorisation.
3) Move on to memorise the basic facts
Memorising means that the student has fast recall without returning to any strategy. This should only come after the students understand the operation, and have some strategies for performing it.
The strategies and understandings that relate to these are very extensive, and are covered in much more detail in the fractional thinking concept map. Students must understand fractions, decimals, and percentages; and that they are different but equivalent ways of representing numbers. Three sets of conversion basic facts follow that are extremely useful for students to instantly recognise. These have strong relationships to the multiplication basic facts up to and including the 10-times table.
The following three links give rise to each of the respective fractional basic facts:
- Tenths, halves, and fifths
- Halves, quarters, and eighths
- Thirds, sixths, and ninths
A) Tenths, halves, and fifths
Each of these only require one decimal place (tenths).
1/10 = 0.1 = 10%
1/2 = 0.5 = 50% (often this is known)
1/5 = 0.2 = 20% (this is less well known, but should be emphasised!)
Table 12 gives the basic fact sets to be recognised. Each row represents equivalent ways of representing the same number. For example 4/10 = 2/5 and 5/10 = 1/2
At the bottom of the table are the related multiplication tables. Note that the 1-, 2-, 5-, and 10-times tables are used.
Table 12 - Tenths, halves, and fifths
|
|
Fraction |
Decimal |
% |
Fraction |
Decimal |
% |
Fraction |
Decimal |
% |
|
|
1/10 |
0.1 |
10% |
|
|
|
|
|
|
|
|
2/10 |
0.2 |
20% |
|
|
|
1/5 |
0.2 |
20% |
|
|
3/10 |
0.3 |
30% |
|
|
|
|
|
|
|
|
4/10 |
0.4 |
40% |
|
|
|
2/5 |
0.4 |
40% |
|
|
5/10 |
0.5 |
50% |
½ |
0.5 |
50% |
|
|
|
|
|
6/10 |
0.6 |
60% |
|
|
|
3/5 |
0.6 |
60% |
|
|
7/10 |
0.7 |
70% |
|
|
|
|
|
|
|
|
8/10 |
0.8 |
80% |
|
|
|
4/5 |
0.8 |
80% |
|
|
9/10 |
0.9 |
90% |
|
|
|
|
|
|
|
|
10/10 |
1.0 |
100% |
1/1 |
1.0 |
100% |
5/5 |
1.0 |
100% |
|
Multiply by |
|
0.1× |
10× |
|
0.5× |
50× |
|
0.2× |
20× |
|
×-table |
|
1× |
10× |
|
5× |
5× |
|
2× |
2× |
B) Halves, quarters and eighths
Each of these require understanding of up to three decimal places (hundredths for quarters, and thousandths for eighths). The following give rise to each of the respective fractional basic facts:
1/2 = 0.5 = 50% because ½ is half of 1
1/4 = 0.25 = 25% because ¼ is half of ½
1/8 = 0.125 = 12.5% because ⅛ is half of ¼
Table 13 gives the basic fact sets to be recognised. Each row represents equivalent ways of representing the same number. Under each column is relate “times table” with the related with the multiplication basic fact (B.F.) under this. Note that the 5-, 25- and the 125-times tables are really useful here.
Table 13 - Halves, quarters, and eighths
|
|
Fraction |
Decimal |
% |
Fraction |
Decimal |
% |
Fraction |
Decimal |
% |
|
|
|
|
|
|
|
|
⅛ |
0.125 |
12.5 |
|
|
|
|
|
¼ |
0.25 |
25% |
2/8 |
0.250 |
25.0% |
|
|
|
|
|
|
|
|
⅜ |
0.375 |
37.5% |
|
|
½ |
0.5 |
50% |
½ |
0.50 |
50% |
4/8 |
0.500 |
50.0% |
|
|
|
|
|
|
|
|
⅝ |
0.625 |
62.5% |
|
|
|
|
|
¾ |
0.75 |
75% |
6/8 |
0.750 |
75.0% |
|
|
|
|
|
|
|
|
⅞ |
0.875 |
87.5% |
|
|
1/1 |
1.0 |
100% |
4/4 |
1.00 |
100% |
8/8 |
1.000 |
100.0% |
|
Mult by |
|
0.5× |
50× |
|
0.25× |
25× |
|
0.125× |
12.5× |
|
× table |
|
5× |
5× |
|
25× |
25× |
|
125× |
125× |
C) Thirds, sixths, and ninths
Each of these require an understanding of recurring decimals. The following four facts give rise to each of the respective fractional basic facts:
1/3 = 0.33333… = 0.3 = 33.3% because 1/3 is a third of 1
1/9 = 0.11111… = 0.1 = 11.1% because 1/9 is a third of 1/3
1/6 = 0.16666… = 0.16 = 16.6% because 1/6 is half of 1/3
9/9 = 0.99999… = 1.0 = 100%
Table 14 gives the basic fact sets to be recognised. Each row represents equivalent ways of representing the same number. Under each column is relate “times table” with the related with the multiplication basic fact (B.F.) under this. Note that the 11.1-, 33.3- and 16.6-times tables are really useful here.
Table 14 - Thirds, sixths, and ninths
|
|
Frac |
Dec |
% |
Frac |
Dec |
% |
Frac |
Dec |
% |
|
|
|
|
|
|
|
|
1/9 |
0.111 |
11.111% |
|
|
|
|
|
1/6 |
0.166 |
16.666% |
|
|
|
|
|
|
|
|
|
|
|
2/9 |
0.222 |
22.222% |
|
|
|
|
|
|
|
|
|
|
|
|
|
1/3 |
0.333 |
33.33% |
2/6 |
0.333 |
33.333% |
3/9 |
0.333 |
33.333% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4/9 |
0.444 |
44.444% |
|
|
|
|
|
3/6 |
0.500 |
50% |
|
|
|
|
|
|
|
|
|
|
|
5/9 |
0.555 |
55.555% |
|
|
|
|
|
|
|
|
|
|
|
|
|
2/3 |
0.666 |
66.66% |
4/6 |
0.666 |
66.666% |
6/9 |
0.666 |
66.666% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7/9 |
0.777 |
77.777% |
|
|
|
|
|
5/6 |
0.833 |
83.333% |
|
|
|
|
|
|
|
|
|
|
|
8/9 |
0.888 |
88.888% |
|
|
|
|
|
|
|
|
|
|
|
|
|
3/3 |
1.000 |
100% |
6/6 |
1.000 |
100% |
9/9 |
1.000 |
100% |
|
Mult by |
|
0.333× |
33.3× |
|
0.166× |
16.666× |
|
0.111× |
11.111× |
|
× table |
|
3 × |
3× |
|
|
|
|
11× |
11× |
Make to 1
Student should be able to automatically recognise when two fractions combine to make 1. This is just an extension of the addition or subtraction basic facts.
Examples:
1/2 + 1/2 = 1, because 1 + 1 = 2 so it is 2/2 = 1
1/4 + 3/4 = 1, because 1 + 3 = 4 so it is 4/4 = 1
3/7 + 4/7 = 1, because 3 + 4 = 7 so it is 7/7 = 1
13/17 + 4/17 = 1, because 13 + 4 = 17 so it is 17/17 = 1
15/11 – 4/11 = 1, because 15 – 4 = 11 so it is 11/11 = 1
Resources
- Tomato harvest
- Patterns and rules II
- Chair and table patterns
- Multiplication rules
- Addition rules
- House patterns
- Exercise programme
- Fitness plan
- Number machines II
- Alpha numeric patterns
- Calculator patterns
- Missing numbers
- Which number?
- Number patterns II
- Chain of numbers
- Finding the rule for the pattern
- What's next?
- Matchstick patterns III
- Growing patterns
- Use the rule
- Growing leaves
- Making triangle patterns II
- Block patterns
- Supermarket patterns
- Training for the cycle race
- Patterns and rules III
- Number machines
- Fitness programme
- More or less
- Number patterns
- Popcorn and juice
- How far will the car travel?
- Morning coffee
- Knitting needles
- Patterns and rules
- Different rules
- Machine rules
- Missing numbers II
- Machines with rules
- Machine rules II
- Missing numbers and rules
- Tukutuku patterns
- Patterns with numbers
Recognising multiplication patterns - factors and multiples
A student should associate each of the sequences, or parts of sequences of times tables with the specific times table.
Example: 3, 6, 9, 12, 15, 18, etc, is the sequence of the 3-times table.
These are the list of the multiples of 3. So each number in this sequence has a factor of 3.
This leads to basic facts for division, as numbers in this sequence must be divisible by 3.
This is the reverse of remembering the basic facts. It is recognising that a number sequence is related to a basic fact.
Square numbers
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, … 400, 900, 1600 …
These should all be known as 12, 22, 32, …, 102, 202, 302, etc
They are: 1 × 1 = 1, 2 × 2 = 4, 3 × 3 = 9, 4 × 4 = 16, 5 × 5 = 25, etc.
It would be useful to recognise 121, 144, 169, 196, 225, 256, 289, 324, 361, and 400 as square numbers for 112 to 202 respectively.
See row 2 of Table 14 for the square numbers
Cubic numbers (and higher dimension)
1, 8, 27, 81, 243, … (The cubic numbers)
These should all be known as 13, 23, 33, 33, etc
They are: 1 × 1 × 1 = 1, 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, 4 × 4 × 4 = 81, etc.
See row 3 for the cubic numbers.
Table 15 Square, cubic, higher dimensional numbers plus power series nd
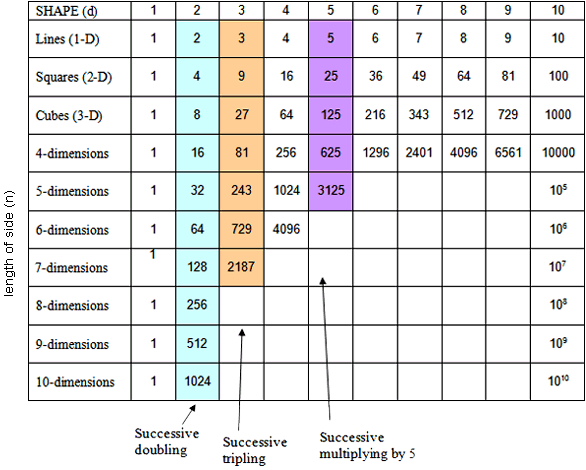
- Successive doubling gives 1, 2, 4, 8, 16, 32, 64, 128, 256 … (see column 2 of Table 14)
- Successive tripling (of) gives 1, 3, 9, 27, 81, 243, … (see column 3 of Table 14)
- Successive multiplying by 5 gives 5, 25, 125, 625, 3125, etc. (see column 5 of Table 14)

