Shading fractions of sets and shapes

Shading fractions of sets and shapes

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about finding fractions of sets and shapes.
a)
Shade \(1 \over 4\) of the set of counters.
 
 
 
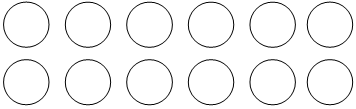b)
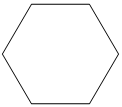
Shade \(2 \over 3\) of each of the three shapes below.
 
 
i) ii)
 
 iii)
c)
Shade \(3 \over 5\) of the set of counters.
 
 
 
   
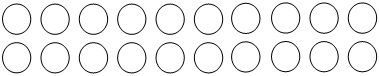d)
Shade \(5 \over 8\) of the grid.
 
 
 
Task administration: 
This task is completed with pencil and paper only.
Level:
3
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Keywords: 
fractions, fractions as operators, sets
Description of task: 
Students find and show given fractions of shapes and sets of counters.
Curriculum Links: 

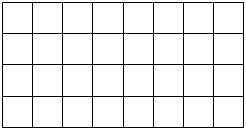Students' strategies, rather than their answers, give a much better indication of the curriculum level and progress. This resource can be used to help to identify students' understanding of fractions as operators. A possible progression for understanding could involve:

  • giving either the numerator or denominator only, suggesting students have not developed a sense of how to find fractions of sets or regions.
  • shading 1/4 of a set only are using simple fractions. 
  • shading 1/4 of a set and 2/3 of 2-3 regions, illustrating that they can find common fractions of regions.
  • finding the fraction of counters and squares in questions c) and d), starting to use early multiplicative working with fractional parts.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Multiplicative thinking, sets 4-5
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
      Y6 (11/2010)
a) 3 counters shaded easy
b) i)

ii)

iii)

 
All 3 shapes correct
2 shapes		 moderate
moderate
moderate

difficult
moderate
c) Shades 12 of the 20 counters. moderate
d) Shades 20 of the 32 squares. moderate
Teaching and learning: 

This resource is about finding fractions of sets (and regions/areas).

Students should be starting to develop an understanding of partitioning and fractions as part-whole relationships. 

We have interpreted that at curriculum level 3 students can begin to use ideas of equivalence or simple multiplicative strategies to find common fractions of sets, quantities or shapes: For example, 3/5 of 30 might involve recognising that 5 lots of 6 make 30, so 1/5 of 30 is 6, and 3/5 would be 3 lots of that. 

Diagnostic and formative information: 

Most students who displayed misunderstandings indicated that they did not see how the top and bottom numbers of a fraction represent a part-whole relationship. They may know some benchmark fractions but did not realise how non-unit fractions are built up from unit fractions. This idea of the part-whole nature of fractions is an important base from which to explore fractions as operators.

  Common response Likely misconception
a) 4 Misconception about the denominator
These students could also simply have no understanding about fractions or have a misunderstanding about the relationship between the denominator and the number of counters. Because they have no understanding of how to find 1/4 of something, the result is that 1/4 of some countable set is 4 (and  1/5 of a set would be 5, etc).

b)

b)

b)

Cannot draw the fraction 2/3
Students draw shaded shapes that may represent other fractions they have worked with previously, such as halves, three-quarters or shading one "piece" or students could not partition into the correct number of parts.

Cannot partition accurately
Students draw conceptually correct partitions to find 2/3 of the rectangle, but the accuracy of their drawing is not sufficient.

Cannot partition appropriately
Students try to draw a rotational type partition to find 2/3 of the rectangle. Although this is theoretically possible to work out thirds in this manner, it really is not an appropriate representation that can be visibly confirmed.
c) 15 Part-whole misconception - finding 3/4 of the set
Students who identified their answer as 15 counters had found 3/4 of the set. Students may know some common fractions and how to apply those as "operators", but cannot work out how much 3/5 of something really is - i.e., three of something that is divided into five parts, or even that it is over half so the estimate should at least be over 10
c)

d)
 

 3 (or 6), or 5 (or 10)

5 or 8
 

 Part-whole misconception - using the denominator or numerator to make some other fraction construct.
Numbers such as 3, 5, or 6 are likely to be guesses, gives the numerator (3) or denominator (5), or the number of counters in 3 or 5 columns (6 or 10 counters, respectively).
For question d) some students simply shaded either the denominator or the numerator as their answer. Students may have recognised that the numerator represents the count of some unit, but students have not moved beyond 5 out of eight of the squares.
c)
d)		 8
13		 Part-whole misconception about fractions - adding the numerator and denominator
Students do not know how the numerator and denominator "work" for fractional numbers (part-whole relationship) and added them together.
Next steps: 

Students who identified that 1/4 of a set of 12 counters was 4 may have confused the two factors (3 and 4) that make up 12, or they may think that a unit fraction of a quantity is determined by the denominator. If this is the case they may need to explore what 1/4 of something actually means (something shared into 4 equal parts) and then show it physically with the 12 counters. Click on the links for two resources that look at the meaning of unit fractions, Fraction shapes, Fractions of sets, or a resource that looks at finding fractions of sets and quantities, Fractions and sets.

Cannot represent the fraction 2/3 or cannot partition appropriately or accurately
These students may have used benchmark fractions that they know, such as halves, unit fractions (like 1/3 , 1/4 , 1/5 , etc) or three-quarters, or simply shading a part (or a piece) of the shape. Other students could not partition into the correct number of parts. These students need to explore partitioning as a first step to understanding how fractions are constructed. Partitioning is an important part of understanding the nature of fractions. Students who could not partition the shapes into appropriate partitions may need to revisit partitioning and look at different types of shapes and justify how they know that the parts are equal-sized and whether they convince somebody else that they are equal sized.
A resource that looks at partitioning and naming fractions of shapes is Sharing shapes. 
Click on the link for more information about partitioning, or resources that explore partitioning.

Part-whole misconception
A Part-whole misconception involves not understanding that the numerator and denominator work together with fractions. Part-whole understanding of fractions involves recognising that a quantity or set or region can be divided into a given number of parts (denominator) and that the numerator is the count of those. Another way of considering the structure of fractions is that the numerator "enumerates" a unit, and that unit is some part of a whole - for 3/5 the unit is 1/5 which is enumerated by 3 (3 lots of 1/5). This idea leads into a way that students can begin to explore fractions of sets, quantities or regions - first partition to find the unit and then enumerate by the numerator. 

Experiences with partitioning can support students' ability to then work with fractions as operators. Until they develop this understanding students are likely to work at trying to construct their own meaning of fractions and as a result create a wide range of additive and multiplicative representations: adding the numbers (numerators and denominators) together, subtracting, multiplying numbers, using only one of the numbers. These part-whole misconceptions become especially evident when students add fractions without recognising that adding requires a common unit, i.e., adding 1/3 and 1/5 is comparable to adding apples and pears. They are different units and cannot be added - hence the need for equivalence.
Click on the link for more information about part-whole fractions, or resources that explore part-whole fractions.

Links to Numeracy (The Number Framework)
Students who can construct and name non-unit fractions are at Stage 5: early additive part-whole (using repeating addition) to Stage 6: Advanced additive (partitioning using division) part-whole.