Fractions and sets

|
a) |
|
 |
|
|
|
|||
|
b) |
|
 |
|
|
|
|||
|
c) |
|
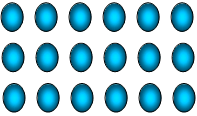 |
|
|
Y4 (11/2006) |
||
|
a) |
i) |
Some way of partitioning the 8 cats into 2 equal groups |
very easy |
|
b) |
i) |
Some way of partitioning the 12 apples cats into 4 equal groups |
easy |
|
c) |
i) |
Some way of partitioning the 18 eggs into 3 equal groups |
easy |
This resource is about partitioning and finding fractions of quantities (and sets).
Students should first have an understanding of fractions as part-whole relationships before beginning to explore how to find the fraction of a quantity (fractions as operators).
Most students who attempted to show how to partition in part i) drew lines to correctly divide the set into the parts required. Across all three questions an average of 24% of students gave the correct solution for the unit fraction, but gave an incorrect solution for the non-unit fraction (11% of students gave the same solution for both fractions).
| Common error | Likely misconception | |
|
a) ii) b) ii) c) ii) |
2 4 3 |
Students do not have an understanding of fractions as part-whole relationships, and simply applied a method of using the denominator to name the fractional part, e.g., 1/2 of 8 is 2; or 1/3 of 18 is 3, irrespective of the quantity the fractional part is the denominator. |
|
a) iii) b) iii) c) iii) |
4 [a) ii) 4] 3 [c) ii) 3] 6 [c) ii) 6] |
Students have calculated correctly for the unit fraction, but could not solve for the non unit fraction. Some believe that only the denominator is used to find the fraction, e.g., 1/4 of 12 is 4 and 3/4 of 12 is 4 implying that 3/4 is no different from 1/4 . |
|
b) iii) c) iii) |
4 or 6 [b) ii) 3] 3 or 9 [c) ii) 6] |
As above, but students are aware that finding the non-unit fraction of a quantity yields a different solution. |
Based on a representative sample of 183 students
Most students who displayed misunderstandings indicated that they did not see how the top and bottom numbers of a fraction represent a part-whole relationship. They may know some benchmark fractions but did not realise how non-unit fractions are built up from unit fractions. This idea of the part-whole nature of fractions is an important base from which to explore fractions as operators.
Students who could not find the unit fraction of the set (including using the denominator as the answer) need to have more experiences partitioning sets and naming the parts (unit fraction) they have created. Ask them to show how they could share the set amongst x [a number of] people –if required give them materials to model this, but encourage them to work with images and towards visualisation. Students beginning to understand fractions should be encouraged to use words to describe the parts, and delay the fractional notation until they have developed some understanding of what fractions represent.
Students who could find the solution for problem with unit fractions only need to explore fractions as part-whole relationships, looking at the different representations of simple fractions (unit and non-unit fractions), and to see how non-unit fractions are built up.
Links to Numeracy (The Number Framework)
Equal sharing of sets or whole numbers simple problems and using a matching strategy is at Stage 4: Advanced counting to Stage 5: early additive part-whole. Students who can construct and name non-unit fractions are at Stage 5: early additive part-whole (using repeating addition) to Stage 6: Advanced additive (partitioning using division) part-whole.
- Sharing Easter eggs
- Buying Christmas presents
- Food fractions
- Food fractions II
- Cookie monster
- Hungry shark
- Soccer season
- Model car fractions
- Counters and fractions
- Money fractions
- Fractions of money
- Fraction Soup
- Tidying up
- Toy holiday
- Food for the day
- Building percentages
- Farm fractions
- Sharing fractions
- Shading fractions of sets and shapes
- Mrs Fletcher's bag
- Tidying Up II
- Fruit Salad

