Cutting the cake
0
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about finding fractions of a shape.
|
a)
|
i)
|
Show how to share a square cake equally between 5 people.
 |
|
| ii) |
How much of the cake does each person get? _____
|
||
|
b) |
i) |
Show how to share a rectangle cake equally between 7 people. |
|
|
ii)
|
How much of the cake does each person get? _____
|
||
|
c) |
i)
|
Show how to share 2 square cakes equally between 3 people.
|
|
| ii) | How much cake does each person get? _____ |
Task administration:
This task is completed with pencil and paper only.
Level:
2
Curriculum info:
Keywords:
Description of task:
Students show how to partition shapes into a given number of equal parts and identify the fraction of each part.
Curriculum Links:
This resource can help to identify students' ability to find and name fractions of sets, shapes, and quantities.
Learning Progression Frameworks
This resource can provide evidence of learning associated with within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.Answers/responses:
| a) |
i)
ii)
|
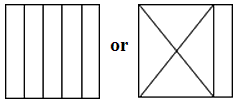
or other partitions that create 5 equal parts.
1/5
|
| b) |
i)
ii)
|
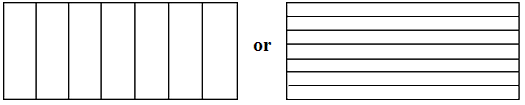 or partitions that create 7 equal parts.
1/7
|
| c) |
i)
ii)
|
 or other partitions that create 3 equal parts. 2/3 or 4/6 or 1/2 + 1/6 (encourage students to give a single fractional name). [Accept a half and a third of a half].
If students answer 1/3 ask if this 1/3 of a (one) pizza or of all the pizza. Probe to get an answer for how much of a pizza.
|
Classroom-based research project about fractions, Y5 class, September 2005
Extension: Get students to explain, compare, and justify the variety of strategies they have used either with the whole class or in a small group. They could look at similarities and differences between the strategies, and identify which are more sophisticated or efficient. Research has shown that students who partition using fewer, larger parts have a more sophisticated understanding of partitioning.
Teaching and learning:
Understanding that shapes, sets and amounts can be partitioned into equal parts is an important piece of knowledge that helps understanding about the part-whole relationship between the numerator and denominator in fractions.
Diagnostic and formative information:
| Common error | Likely misconception | |
| a) & c) |
 |
Students do not understand partitions should be equal. Either students do not recognise that the pieces have to be equal or are aware that the pieces must be equal but cannot construct the correct angles to make them equal. The possible overuse of pizzas as their only representation of fractions may lead to this. |
| b) |
 |
Students create one more partition than required. Students include the partition for the one (numerator) and create 1 + 7 partitions. This could be a misconception based around either prior learning to construct a ratio 1:7 or a miscount while trying to construct the partitions, .i.e., students count the lines instead of the parts. |
| c) | 1/3 |
Students give the fraction of both cakes not one cake. They are treating both cakes as the whole rather than a single cake. The language here is important as it distinguishes what the whole is. This is idea of the part and the whole and the relationship between them is essential to understanding fractions. |
Next steps:
Some students have had limited experiences with fractions and partitioning and rely on the methods of cutting up they are familiar with. If they have only ever divided up "pizzas" (or other shapes with rotational symmetry) they may think this is the only way to divide shapes up. Using a cake which can be cut in many different ways or square pizzas can be used to challenge the students' concept of circular representations of fractions. Partitioning becomes more difficult when the partitions cannot be derived by a halving strategy, or the shapes are more complex and cannot easily be overlaid to check for equal-size. It is also important to encourage students to explain how they know the partitions are even, and how they could justify this to somebody else (they may need to fold, or cut and overlay the pieces).
It is important that students build up many experiences of partitioning starting with…
- halving of basic shapes, then halving multiple times to derive other parts;
- partitioning a variety of shapes: squares, two squares, rectangles, circles, hexagons (which are easier to partition accurately than circles), etc.
- partitioning shapes into a different number of pieces (e.g., 3, 5, 6, 7, 9, etc).
By partitioning shapes into odd numbered parts and with a range of shapes, students develop a more robust understanding of partitioning. This variety ensures that they are not only remembering partitions with certain shapes, but that they are developing a strategy to represent and understand fractions and can partition any simple shape, recognising that these parts should be equal-sized.