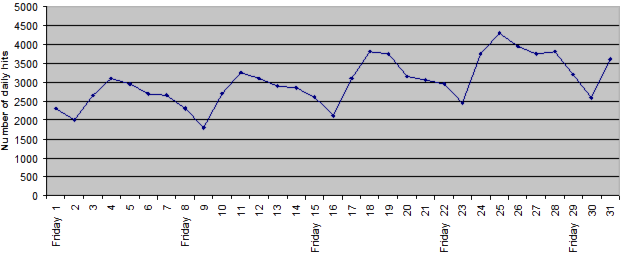
Website hits

Website hits

Pencil and paperOnline interactive
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about reading information from a time-series graph.
 Plan-Ahead website
 
Website-hits-graph-for-Plan-Ahead.png
May 2021
This graph shows the number of daily hits on the Plan-Ahead website for May.

Question 2Change answer

Several people made comments about the graph. 
a)  Select whether these statements about the month of May are True or False.
 
     i)    "There was no pattern to the number of hits during May."                         TrueFalse
     ii)   "The number of hits on the website increased overall during May."          TrueFalse
     iii)  Monday is the most popular day for using the website.                             TrueFalse
     iv)  "The fewest hits were on Saturday, 2nd May."                                           TrueFalse
     v)   "The pattern repeated on a weekly basis."                                                  TrueFalse

Question 2Change answer

b)  Give your own description of the most important features that the graph shows about the hit rates during May 2021 on the Plan-Ahead website.
Task administration: 
This task can be completed with pencil and paper or online (with SOME auto-marking).
Level:
5
Curriculum info: 
Maths, Statistics, Statistical literacy
Key Competencies: 
Using language, symbols, and texts
Keywords: 
time-series, graph interpretation, trend, cycle, work samples
Description of task: 
Students identify true and false statements, and provide a description of the most important features of a time series graph.
Curriculum Links: 
Key competencies
This resource involves describing the key features of a time series graph. This relates to the Key Competency: Using language, symbols and text.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Interpreting statistical and chance situations, set 5
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
      Y10 (06/2009)
a)

i)

ii)

iii)

iv)

v)

False

True

True

False

True

very easy

very easy

very easy

very easy

very easy
b)

 

 

Writes a description that includes both these features:

Any 1 of:

  1. There is an upward trend in the number of hits; and
  2. There is a weekly cycle, including:

    1. Describing the cycle
    2. Mentioning there is a weekly cycle; or
    3. that both Monday is the most popular day, and Saturday day is the least popular.

Mentions just one of:

  1. the upward trend in the number of hits; or
  2. the weekly cycle, including:

    1. Mentioning there is a weekly cycle;
    2. Describing the cycle; or
    3. Both of "Monday is the most popular day", and "Saturday day is the least popular".

both features - moderateone feature - very easy
Based on a representative sample of 144 Y10 students.  

NOTE: Students were not credited with commenting on the cyclical nature of the graph if they mentioned just one (but not both) of: "Mondays have the highest number of hits" or "Saturdays have lowest the number of hits."  The former of these merely reiterates one of the initial statements in part a). If students mentioned both, this was seen as evidence of seeing the cycle.

Examples of student responses that mentioned both the weekly cycle and the upwards trend (30 students had both).

  • [It] shows the general increase while also containing its own weekly cycle.
  • The number of hits rapidly increased then slowly dropped over the week but grew more each [subsequent] week.
  • The hits increased mostly during May and the graph had a pattern over each week.

Examples of student responses that described the weekly cycle but not the trend (41 students)

  • The number of hits went up during the weekend and Monday. After that they slowly decreased until the next weekend.
  • The number of hits dropped on Saturdays and peaked on Mondays.
  • Monday is the most popular day and the pattern repeated. 

Examples of student responses that described the upwards trend but not the cycle (13 students):

  • The rates increase every week in May.
  • The amount of people visiting the website is increasing each week.
Teaching and learning: 

This resource is about responding to claims made about a graph. Responding to statistical claims is called "statistical literacy". Students should also be able to identify and describe the major overall information that a graph shows. The two main features of this time series graph are:

  1. There is a cycle (or pattern) that repeats each week.
  2. There is an upward trend in the graph.
Diagnostic and formative information: 
  Common responses that ignore the two major data features of this graph
b) Makes statements about the readability of the graph. Examples:

  • The hits are plotted for every day;
  • The dots are joined by lines;
  • There are horizontal grid lines.
b) Gives features that good graphs should have. Examples:

  • It has a title;
  • The axes are labelled;
  • The axes have linear scales.
b) Makes statements about the readability of the graph. Examples:

  • May 25th has the most hits;
  • May 9th has the least hits;
  • There were 3000 hits on May 4th;
  • Every day had more than 1700 hits.
Next steps: 
Gives features that good graphs should have or Makes statements about the readability of the graph
These responses may very likely reflect the sorts of tasks the students are asked to do in class. They need to look at the "big overall picture" that a graph gives, not the detailed component parts.
  1. Ask the student to say something important about the overall patterns of this graph, not just statements about particular points on the graph.
  2. If they cannot, give them leading questions such as:a) Tell me what has happened each Monday? Each Saturday? Each of the other days?b) How did early May hit levels compare with those in late May?
  3. Place a transparent ruler over the graph, and ask students what they now notice. Allow them to move it around until they find a "line of best fit". This should slope upwards, and the weekly cycle should become even clearer.

Gives correct statements about the graph that ignore the weekly cycle or upwards trend

  1. Assure the student that they have made a correct statement.
  2. Ask them if they can say something else that summarises the whole graph (i.e. all the points plotted on it) rather than just one point on the graph.
  3. If they can not, give them leading questions such as:a) Tell me what has happened each Monday? Each Saturday? Each of the other days?b) How did early May hit levels compare with those in late May?

Students who correctly identify the trend and the cycleChallenge them to:

  1. Suggest why the weekly cycle or the upwards trend may have occurred.
  2. Give ways in which the graph may be used. (See the box below entitled Responses that show extra insight.
  Responses that show extra insight
b) Gives a reasonable explanation about why there is a weekly cycle. Examples:

  • It is a family day;
  • The weekly planning is done then.
b) Gives a reasonable explanation about why there is an upwards trend. Example:

  • More people know about the site.
b) States what can be done with as a result of the graph. Examples:

  • Put out new releases on a Monday because lots of people will see it;
  • [You could] predict how many people will be using the site in the future;
  • Use it for planning purposes.

NOTE: These responses were uncommon and were not asked for, but show good insight into making inferences from a graph. Discussing these inferences might be a way to help students make meaning of the graph.

Figure it out
Mad Minute Statistics Book One L4+, pages 6 to 7 gives an example of an upwards trend.