Addition and Subtraction Concept Map

Component: 
Introduction
Addition is typically the first and the simplest mathematical operation that students meet. It has a very close cousin in subtraction, which is generally somewhat harder for students.
This concept map includes addition and subtraction of whole numbers and decimal fractions, as well as negative numbers. It does not include fractions.
 
For most of this concept map, the principles will be demonstrated using whole numbers, i.e., the numbers {0, 1, 2, 3, 4, ….}. These principles also apply to decimal numbers and to negative numbers.
 
Often when we encounter addition we look at problems such as 9 + 4 = □ , where □ is the amount we want to find (often referred to as the "unknown"). It is important to explore the variety of ways that addition number sentences can be written, because this help students be more adaptable and it assists them to think more algebraically.
For more see Forms of addition and subtraction number sentences.
Types of word problems
There are four different ways that we can think about addition or subtraction word problems.
 
Change problems
When we think of addition we most often think of problems where there is an initial number of objects, and some more
objects are added to it. These are called change problems. For subtraction there is an initial number of objects, and some
are removed. The problem is dynamic - a change is indicated.
Examples:
Abi has 8 marbles. She gets 6 more. How many marbles does she now have?
This can be written as 8 + 6 = □. 
A set with 8 marbles is joined with a set of 6 marbles.
 
Abi has 14 marbles. She gives 6 away. How many marbles does she now have?
This can be written as 14 – 6 = □. 
A set with 14 marbles has 6 marbles taken away (separated off).
 
 
Combine problems
This is where we have two groups which together comprise a whole. The problem is static as there is no change involved.
Example:
 
Abi has 8 red marbles and 6 green marbles. How many marbles is this? 
This can be written as 8 + 6 = □.
A set of 14 marbles is a combination of 8 red and 6 green marbles.
 
Relevant resource: Saving for a pet
 
Compare problems
This is when the size of two different numbers are compared. Words such as "more" or "less" are used.
Again, it is a static problem, as the numbers are already determined.
Examples:
Ben has 5 marbles. Abi has 9 more marbles than Ben. How many marbles does Abi have?
This can be written as 5 + 9 = □
 
Abi has 14 marbles. She has 9 more than Ben How many marbles does Ben have?
This can be written as 14 – 9 = □
 
Relevant resource: Going on camp part (d)
 
Equalize problems
This is a mix of a compare problem and a change problem. It poses the question
"What change is needed to make two numbers equal?"
It is more of a dynamic question, as it looks at a potential change.
Examples:
Ben has 5 marbles. If he buys 9 more marbles, he will have the same number as Abi.
How many marbles does Abi have?
This can be written as 5 + 9 = □
 
Abi has 14 marbles. If she gave away 9 marbles, she would have the same number of marbles as Ben.
How many marbles does Ben have?
This can be written as 14 – 9 = □
 
Relevant resource: Collecting beads part (b)
 
In each of the examples given, the number sentences are of the form: a + b = □ or c – b = □
These use the equals sign (=) in the rather naïve sense "and the answer is".
For other ways number sentences can be written see the next section, Forms of addition and subtraction number sentences.
Forms of addition and subtraction number sentences
When we are solving addition or subtraction problems, we are trying to find out a missing number (represented by the symbol □) that will make the number sentence true.
For example, in the sentence 8 + 6 = □, we are trying to find out the value of □ that will make the equation true. In this case, □ = 14.
The different forms that number sentences have can be classified and named as follows:
 
Addition sentences
There are three different positions that the "□" can be located in.
Sentence  Example Name of problem
8 + 6 = □  Abi has 8 marbles, and she gets 6 more. How many marbles does she now have? Missing sum (Often called the "canonical form")
8 + □ = 14  Abi has 8 marbles. How many more does she need so she has 14 marbles? Missing addend
□ + 6 = 14 
Abi has some marbles. She gets 6 more to give her a total of 14 marbles.
How many marbles did she have to start with?
 Missing augend 
 
The names used are based on an often forgotten set of terms for the component parts of addition problems.
Augend + Addend = Sum
Missing sum problems are usually easiest for students, missing augend problems are the hardest, with missing addend problem
somewhere between. Missing addend or missing augend problems lead students to a more algebraic way of thinking.
It is not imperative to remember these naming conventions, and it may be counter-productive to introduce them to students.
 
Subtraction sentences
There are three different positions that the "□" can be located in a subtraction sentence.
Sentence  Example Name of problem
14 – 6 = □  Abi has 14 marbles. She gives 6 away. How many marbles does she now have? Missing difference (Often called the "canonical form")
14 – □ = 8  Abi has 14 marbles. How many does she need to give away so she has 8 marbles? Missing subtrahend
□ – 6 = 8  
Abi has some marbles. She gives 6 away and is left with 8 marbles. How many marbles did she have to start with?
 Missing minuend
 
The names are based on an often forgotten set of names for the component parts of subtraction problems.
Minuend – Subtrahend = Difference
The missing difference problems are generally the easiest for students, and the missing minuend problems are the hardest.
Missing subtrahend or missing minuend problems lead students to a more algebraic way of thinking.
It is not imperative to remember these naming conventions, and it may be counter-productive to introduce them to students.
 
Location of the equals sign
It is also useful to keep in mind that the location of the equals sign can change.
Example:
Abi has some marbles. 8 are red and the other 6 are green. How many marbles does she have altogether?
This can be written as □ = 8 + 6
 
Expose students to problems of each form, and with different locations of the equals sign. This will help them develop a much
richer view of the equals sign and will also help with algebra. See Algebraic thinking concept map (equality), or Equations and expressions for more.
 
Relevant resources:
The majority of ARB resources are missing sum or missing difference problems.
Missing augend or minuend: Buying some things, Subtraction wheel
Relationship between addition and subtraction (Macro-jumps)
Addition and number sentences can be represented by movements on the numbers line. A macro-jump represents the actual number sentence with one single jump. This can then be broken down into several smaller jumps (micro-jumps) which reflect the actual strategy being – see Strategies for addition and subtraction (Micro-jumps).
Addition and subtraction are closely related. Subtraction can be thought of as the opposite of addition. Subtraction, however, is often harder for students than addition. Subtraction sentences can often be changed into equivalent addition sentences (or vice versa) using a process known as "reversal". This involves rearranging a number sentence and reversing the direction of the jump on a number line that represents the number sentence.
Examples of useful reversals (see the table that follows).
  1. 143 – □ = 81 is equivalent to 81 + □ = 143
  2. □ – 62 = 81 is equivalent to 81 + 62 = □
  3. □ + 62 = 143 is equivalent to 143 – 62 = □ or 62 + □ = 143
Reversal uses the properties of addition, particularly the additive identity and additive inverse properties. This is an algebraic way of thinking, rather than purely number. For more see Properties of addition and subtraction, or the section Additive identity - Applying the property – Algebraic thinking concept map.
 
Using reversal
  • It can make solving some number sentences easier.
  • The arrows in the table (← ←) show the direction of reversal that is typically most useful.
  • Reversal is often used in solving algebraic expressions (e.g., x + 3 = 7 ↔ x = 7 – 3)
Table different forms of addition or subtraction
Addition  Subtraction Addition number line                 Subtraction number line
81 + 62 = □ ←
(missing sum)		 ← □ – 62 = 81
(missing minuend)		 NL 1.png
81 + □ = 143 ←
(missing addend)		 ← 143 – □ = 81
(missing subtrahend)		 NL 2.pngNL 3.png
□ + 62 = 143 →
(missing augend)		 → 143 – 62 = □
(missing difference)
or
→ 62 + □ = 143
(missing addend)		 NL 4.png
 
 
Students should not be given hard and fast rules for which form of the number sentence they should use. Encourage them to use ones that are most intuitive to them. This may differ from student to student. 
 
Use reversal to keep the jumps small
Strategies are often more efficient when making the smallest jump possible.
Some useful reversals are shown below:
Addition
  • Missing sum:
751 + 62 = □ Keep as is because the jump is small.
62 + 751 = □ → 751 + 62 = □ This is the same principle as counting on from the bigger number.
  • Missing addend:
751 + □ = 813 Keep as is because the jump is small.
62 + □ = 813 → 813 – 62 = □
  • Missing augend:
□ + 62 = 813 → 813 – 62 + □
□ + 751 = 813 → 751 + □ = 813
 
Subtraction
  • Missing difference:
813 – 62 = □ Keep as is because the jump is small.
813 – 751 = □ → 751 + □ = 813
  • Missing subtrahend:
751 + □ = 813 Keep as is because the jump is small.
62 + □ = 813 → 813 – 62 = □
  • Missing minuend:
□ + 751 = 813 → 751 + □ = 813
□ + 62 = 813 → 813 – 62 + □
 
Do NOT use these as hard and fast rules. The choice on whether to change a number sentence often depends on the actual numbers in the problem. Let the student use the form of the problem which is most natural to them. They may also be exposed to other ways of seeing the problem through discussing other students' approaches to the problem.
Strategies for addition and subtraction (Micro-jumps)
This section explores the different ways that jumps can be made, i.e., it breaks the single macro-jumps that were mentioned in the previous section down into a series of smaller jumps. This section gives a brief look at the different strategies used at different stages of the Number Framework. More detail is given in Book 5: Teaching Addition, Subtraction, and Place Value [pdf]. These strategies are particularly useful for estimating the answers to problems. For more on estimation in general, see the Computational estimation concept map.
 
Stage Addition Subtraction
Stage 1-3
Counting from 1
5 + 4 = □
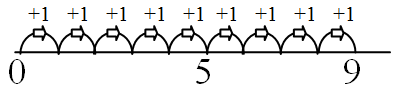NL B.png
Counts out 5 and then another 4, then counts all the objects.
9 – 5 = □
Counts out 9 objects, takes away 5 objects and then counts the remaining objects.
Stage 4 
Advanced Counting
8 + 5 = □
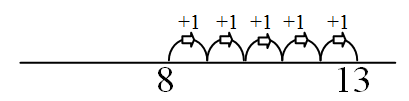
NL B2.png
Starts at 8 and counts on by 5.
13 – 5 = □
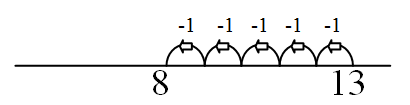
NL A.png
Starts at 13 and counts back by 5.
Stage 4
Advanced Counting moving to Early Additive.
27 + 24 = □
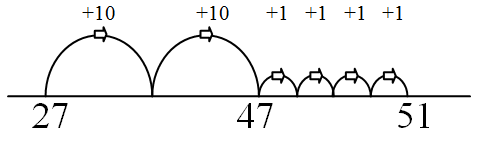NL C.png
This involves counting on from the bigger number, but still incrementing in 1's and 10's
38 ­– 23 = □
NL D.png
Again, this is starting from the bigger  number, but counting back in 1's and 10's.
Stage 5
Early additive Part-whole
8 + 5 = □
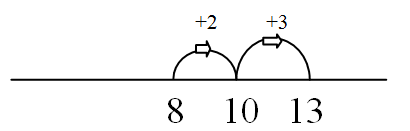NL F1.png
Bridging 10 using part-whole

37 + 23 = □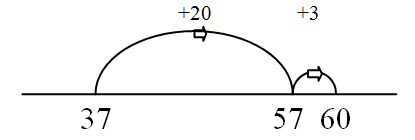
NL G1.png
Place value jumps by tens then ones

38 + 54 = □

Bridging 10
 13 – 5 = □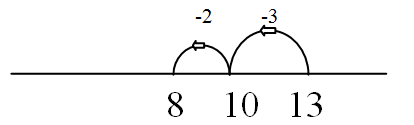
NL F2.png
Bridging 10 using part-whole
 
60 – 23 = □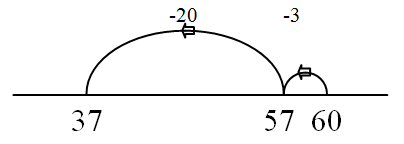
NL G2.png
Place value jumps by ones then tens
 
Stage 6
Advanced additive (Early multiplicative Part-whole) 
16 + 18 = □
NL-addition-B.png
Rounding and compensating
 
15 + 23 = □
= (15+3) + (23–3)
= 18 + 20
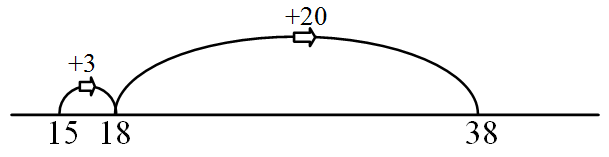
NL-addition-C.png
Equate using additive identity (3 – 3 = 0)
 
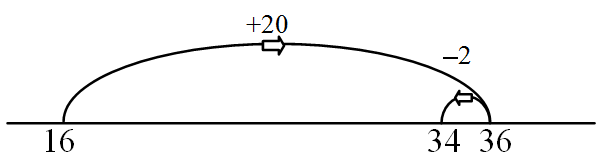
127 + 126 = □
= 127 + 100 + 30 – 4
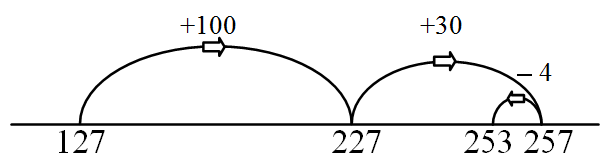
NL-addition-D.png
Mix of strategies
37 – 18 = □
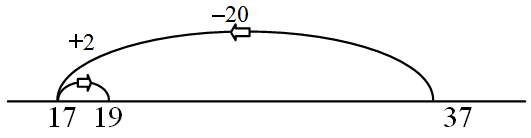
NL-subtraction-F.png
Rounding and compensating
 
33 – 17 = □
= (33+3) – (17+3)
= 36 – 20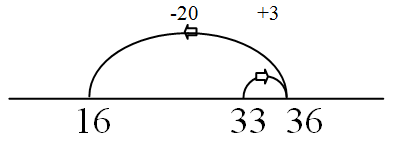
NL L2.png
Equate using additive identity (3 ­– 3 = 0)
(also called "Equal addition")
Stage 7 Early multiplicative Using the above strategies with decimal numbers. Using the above strategies with decimal numbers.
 
Relevant resources
 
In depth information on the use of different strategies:
 
Place value partitioning (PVP) strategies and the vertical algorithm
PVP and addition
The preceding strategies are useful for adding pairs of numbers that are relatively small - generally up to three-digit numbers. Place value partitioning is suitable for adding several numbers, including larger ones. It breaks each number down into each of its place value components (ones, tens, hundreds, etc.)
Example:
973 + 868 = (900 + 800) + (70 + 60) + (3 + 8) = 1700 + 130 + 11 = 1841
 
PVP and addition algorithm
Place value partitioning relates directly to the standard addition algorithms. Initially students should work with Examples A, C and E, which make the relationship explicit. They can then move to the "carrying" models in Examples B, D and F (the bolded amounts in Examples A, C and E are written as superscripts in Examples B, D and F). Examples 5 E and F come from Book 5 of the NDP, pp 64 - 65
Examples:
 
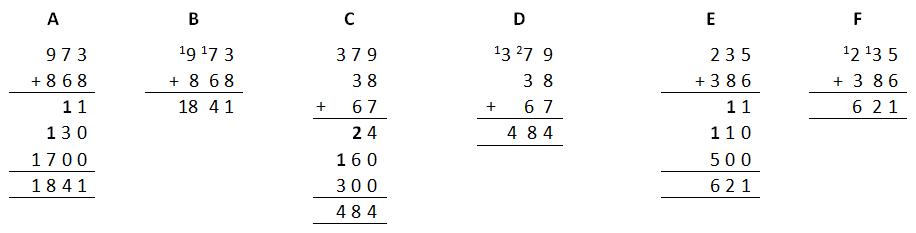
examples-vertical-algorithm.png
PVP and subtraction algorithm
Place value ideas assist students to develop a standard subtraction algorithm. The standard PVP can often lead to dealing with negative numbers.
Example:
563 – 287 = (500 – 200) + (60 – 80) + (3 – 7) = 300 + –20 + –4 = 276
 
Subtraction algorithm
The concept of renaming is used to avoid these negative numbers; for example, 56 is 40 + 16. This may need to be repeated for tens and hundreds, etc.
Example of subtraction algorithm (See NPD Book 5, p. 65)
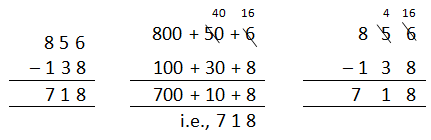
examples-vertical-algorithm-ii.png

Resources

Decimal numbers

Decimal place value understanding

Before students add or subtract decimals, they need to understand the place value structure of decimal numbers. Decimal numbers just extend the place value concept from larger numbers (tens, hundreds, and thousands etc.) to numbers closer and closer to 0 [tenths (1/10), hundredths (1/100),
thousandths (1/1000) etc.]. In each case it takes 10 of the smaller unit to make one of the larger unit. The pattern below show part of this. The pattern can continue infinitely often, with numbers getting closer and closer to 0 (e.g., 0.000001), or getting bigger and bigger (e.g., 10,000,000).
 
  0.001 is 1 thousandth = 1/1000
Ten 0.001's make 0.01  0.01 is 1 hundredth = 1/100
Ten 0.01's make 0.1 0.01 is 1 tenth = 1/10
Ten 1's make 10  10 is 1 lot of ten, and 0 ones
Ten 10's make 100 100 is 1 lot of a hundred, 0 tens and 0 ones
Ten 100's make 1000  1000 is 1 lot of a thousand, and 0 hundreds, tens, and ones
 
The place value nature of decimal numbers can also be displayed using a six-pronged abacus to represent the whole numbers (Hundreds, Tens and Ones) and decimal numbers (tenths, hundredths, thousandths etc).
 
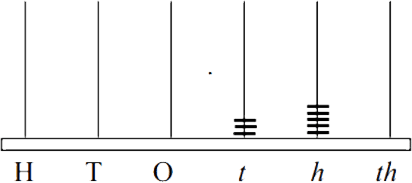
decimal-number-abacus.png
​​
Students need to be able to understand place value structure of decimals, preferably up to 2 or 3 decimal places. They should also able work with decimals with different numbers of decimal places. They may be able to order decimals with the same number of decimal places but still treat them as
whole numbers (e.g., 0.32 is treated like 32). For example, they may think "0.32 is larger than 0.4 because 32 is larger than 4". They could then think that 0.32 + 0.4 = 0.36.
 
Relevant resources
Understand the place value structure of decimals, preferably up to 2 or 3 decimal places: Changing fractions to decimals, Writing words, or Writing decimal numbers
 

 

Operating (+ and –) on decimal numbers

Once students have a firm grasp on the place value meaning of decimal numbers, all the strategies that were used with whole numbers are the same with decimal numbers. For example, use "carrying" when crossing decimal boundaries.
 
Examples:
 
2.7 + 3.5 = (2 + 3) + (0.7 + 0.5) = 5 + 1 + 0.2   Place value partitioning
2.7 + 3.5 = (2.7 + 0.3) + 3 + 0.2 = 3 + 3.2 Bridging 1 using part-whole
2.7 + 3.5 = 2.7 + 3 + 0.5 Place value jumps
Relevant resources which use decimals numbers
Subtraction: Temperature changes
 
There are quite a number of addition and subtraction resources involving money. These are often handled well by students, but this may overstate their ability to add or subtract decimals as the cents represent a whole number of cents. Money uses just tenths (10 cents) and hundredths (1 cent). The latter coins (1¢, 2¢ and 5¢) are no longer in circulation. You can, however compute to fractions of a cent, so $12.375 is possible). There still is, of course, the opportunity to rename cents as dollars.
2.7 + 3.5 = (2 + 3) + (0.7 + 0.5) = 5 + 1 + 0.2  

Resources

Negative numbers
As soon as we subtract numbers, the possibility of encountering negative numbers arises.
Example: 5 – 3 = 2, but what does 3 – 5 equal? The answer is  ¯2.
So what is ¯2?
  • It can be thought of as "two less than zero"
  • It can also be thought of as "the opposite of 2". This is because 2 + ¯2 = 0. Both + 2 and ¯2 are the same distance from 0 on the number line.
Understanding negative numbers {number and algebra;number knowledge; negative numbers}
The number line is an excellent way to approach negative numbers. These are all the numbers that are to the left of zero (or below it on a vertical scale, such as a thermometer.
Numbers are either:
  • Positive (bigger than zero and to the right of zero on the number line). Example: 5 (which can be written + 5)
  • Negative (smaller than zero and to the left of zero on the number line). Example: ¯5 (which is called "negative 5" or "the opposite of 5")
  • Zero (0)
Notice how a negative number has a negative sign that is written as a superscript. The sign is part of the number.
It is different from the subtraction symbol "–", which is an operation (e.g., 5 – 3). We can also have a mix of operators and negative signs (e.g., ¯5 – 3, 5 + ¯3).
Negative numbers can be either integers or decimal numbers (e.g., ¯7 or ¯3.45)
 
NL negative.png

Real examples of negative numbers

Temperatures: In winter, the temperature falls below 0°C. (see Ordering temperatures).
Water level: This could be set at "sea level". Depths below this are negative (see Water level).
Money: If I have some money, it is positive, e.g., $10. If I owe some money, I have a negative balance, e.g., $ ¯5 (i.e., I owe $5).
Games: If points are deducted, then a score can be negative (see House points)
 

Adding and subtracting with negative numbers

Subtraction can be thought of as the opposite of addition. Subtraction undoes addition. For example (150 + 5) – 5 = 150
There are four types of addition and subtraction problems. For each of these, the starting and finishing point can be a positive or a negative number.
  • Add on a positive number to any number. This makes a larger amount (e.g., 5 + 3 = 8, ¯3 + 5 = 2, ¯5 + 3 = ¯2)
  • Subtract a positive number from any number. This makes a smaller amount (e.g., 5 – 3  ¯3 – 5 = ¯8, 3 – 5 = ¯2)
  • Add on a negative number to any number. This makes a smaller amount. (e.g., 5 + ¯3 = 2, ¯3 + ¯5 = ¯8, 3 + ¯5 = ¯2)
  • Subtract a negative number from any number. This makes a larger amount. (e.g., 5 – ¯3 = 8, 3 – ¯5 = 8, ¯3 – ¯5 = 2)
This leads to two rules:
1. p + q = p – – q Adding a positive number has the same effect as subtracting a negative number. (e.g., 5 + 3 = 5 – ¯3 = 8)
2. p – q = p + – q Subtracting a positive number has the same effect as adding a negative number. (e.g., 3 – 5 = 3 + ¯5 = ¯2)
These can be demonstrated using the bucket balance model (See Numeracy Development Book 5, pp. 74-75)
Another similar model could be a basket with helium balloons (which give a positive lift) and weights (which drag it down – a negative effect).
1. Add a balloon (+) and the basket will rise. Take away a weight (–) and the basket will rise.
2. Take away a balloon (+) and the basket will drop. Add a weight (–) and the basket will drop.
 
Visualising with the number line
Students can use a number line to help them visualise if the result of an addition or subtraction is positive or negative.
In some cases, the result is the opposite sign from the initial number (e.g., ¯3 + 5 = 2, 3 – 5 = ¯2)
In other cases, the sign may stay the same (e.g., ¯5 + 3 = ¯2, ¯3 – 5 = ¯8)
 
Students need plenty of practice with this, including different combinations of positive and negative numbers, using subtraction as well as addition.
This is essential to help the transition from number to algebraic thinking.

Some useful rules for negative numbers

Some of these have already been seen in the section Adding and subtracting with negative numbers.
Rule Rule Example
Subtraction as addition p – q = p + ¯q  4 – 3 = 4 + ¯3
Addition as subtraction  p + q = p – ¯q  4 + 3 = 4 – ¯3
Addition is the inverse of subtraction
 (p + q) – q = p and
(p - q) + q = p 
(5 + 3) - 3 = 5
(5 - 3) + 3 = 5
– (q –p) is the inverse of (p – q) p – q = ¯(q –p) 9 – 5 = ¯(5 – 9)
Inverse element ( – p is the inverse of p) p + ¯p = 0, p – p = 0 9 + ¯9 = 0, 9 – 9 = 0
    
We could swap the more technical word "inverse" for the more accessible word "opposite".
Properties of addition and subtraction
Many of these properties will have been referenced earlier in this concept map. Many of these properties are taken for granted, but it is worth spelling them out. Some of the properties do not apply to subtraction. These properties hold for all types of numbers used in primary and junior secondary schools. [for more information on numbers, see Types of Numbers]
 
Property Name Addition   Subtraction  
Commutativity p + q = q + p  9 + 5 = 5 + 9 p – q ≠ q – p   9 – 5 ≠ 5 – 9
Associativity p + (q + r) = (p + q) + r   9 + (5 + 2) = (9 + 5) + 2 p – (q – r) ≠ (p – q) – r  9 – (6 – 2) ≠ (9 – 6) – 2
Identity element (0) p + 0 = p   9 + 0 = 9 p – 0 = 0 9 – 0 = 9
Inverse element ( ¯ p) p + ¯ p = 0 9 + ¯ 9 = 0 p – p = 0     9 – 9 = 0
Cancellation law  If p + x = q + x then p = q     p + x = q + x then p = q p – x = q – x then p = q
Closure law  The sum of 2 numbers is always a number   The difference between two numbers is always a number  
    
Even though commutativity and associativity do not work for subtraction, we can turn subtraction into addition by taking the opposite of the numbers.
Examples:
9 – 5 = 9 + ¯ 5 = ¯5 + 9
9 – 5 – 2 = 9 + ¯5 + ¯ 2 = 9 + (¯5 + ¯2) = (9 + ¯ 5) + ¯ 2
Common misconceptions
Compacting hundreds, tens and ones (compact numerals)
  • Combines the hundreds and tens and ones to make a number.  These errors can generally be recognised by "large" numbers with lots of zeros.
               Example: 100 + 34 "=" 10034
Counting errors (often get close to the correct answer)
  • Starts the first count with the actual number rather than the next number. Gets an answer 1 short of the actual answer.
               Example: 8 + 5 "="12 [goes 8, 9, 10, 11, 12 instead of 9, 10,11, 12, 13]
  • Does not keep track of the count efficiently. Gets an answer a few short of or a few more than the actual answer.  Usually occurs for larger counting on sequences.
              Example: 38 + 25 "=" 61, 62 or 64, 65 
These errors most commonly occur on the 1's digit, but can also happen on the 10's, 100's, etc.
 
Relevant resources: School vege garden, Vegetable soup
 
Crosses the 10's and/or 100's boundaries incorrectly — Failure to "carry" (usually out by 10, 100 etc)
  • Students added digits together but did not take into account place value issues moving from ones to tens; tens to hundreds; hundreds to thousands etc.
    In the vertical algorithm this is referred to as not "carrying the ten". It also occurs with place value partitioning (the horizontal form , i.e., (30 + 20) + (8 + 5).              
                Example: 38 + 25 "=" 53 (instead of 63)
 
Relevant resource: Solving maths problems     
  • Students do not group numbers together correctly with place value partitioning.
    This occurs with numbers of different orders of magnitude. This is equivalent to not aligning numbers correctly using the vertical algorithm.
               Example: 342 + 25 "=" 592 – Calculates (300 + 200) + (40 + 50) + 2 instead of: 300 + (40 + 20) + (2 + 5)
 
Relevant resource:Saving for a pet
 
Errors with decimals: Treating decimals as whole numbers
  • Students add the decimal fractions as if they were whole numbers.
              Example: 3.8 + 2.5 "=" 63 (or 0.63)
Relevant resource: Weighing for the post
 
Place value error: recombining decimals
  • Students add the decimal fractions but make an error recombining the tenths: either carried over to a newly created decimal place before the tenths

    or do not carry at all.
               Examples: 3.96 + 2.04 "=" 5.100
                                3.57 + 2.66 "=" 5.123 (or 5.113 - not "carrying" hundredths)
Relevant resource: Weighing for the post
 
Promotional Text: 
Alex Neill and Jonathan Fisher, 2015