Building percentages

Building percentages

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about finding percentages of whole numbers.

Below is a diagram of a building.

a) If the total height of this building is 30 metres, work out the height for 50%, and 25% of the total. 
Write your answer in the box opposite the percentage.
 

 

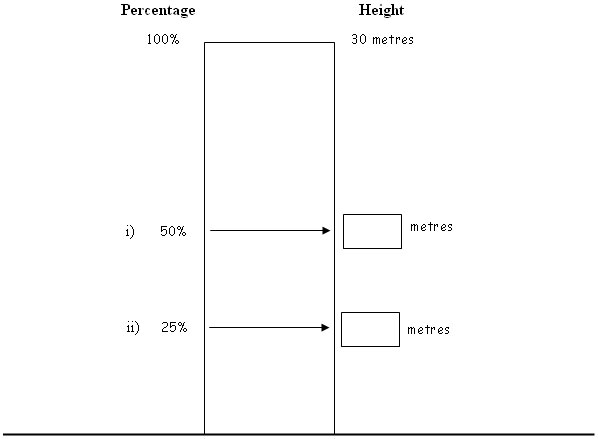
b) Explain or show what you would do to find 75% of the height of the building.
 
 
 
 
 
 
 
 
 
Task administration: 
This task is completed with pencil and paper only.
Level:
3
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Keywords: 
percentages, double number lines, halving, fractions as operators
Description of task: 
Students use percentages to calculate heights of a building from the total height. They then explain how to calculate another percentage.
Curriculum Links: 
This resource can help to identify students' ability to apply simple multiplicative strategies to find fractions or simple percentages of sets, shapes, and quantities.
 
Key competencies
This resource involves recording the strategies students use to find fractions or percentages of sets, shapes, and quantities. This relates to the Key Competency: Using language, symbols and text.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Multiplicative thinking, sets 4-5
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
      Y6 (11/2007)
a) i)
ii)		 15
7.5		 easy
moderate
b)   Explanation illustrating how they broke the total into component parts by finding a basic unit and multiplying or adding as required; or methodology for computation. [solution is not required]. Accept any 1 of:

  • multiplying 25% by 3;
  • adding 25% to 50%;
  • subtraction 25% from 100%;
  • adding the actual numbers from, i.e., 15 + 7.5;
  • other correct methods.
 easy

Based on a representative sample of 167 Y6 students.

Teaching and learning: 
This resource is about using a double number line to support finding percentages of numbers.  It lends itself to a doubling and halving strategy, other partitioning as the numbers and students' ability permit, and provides a way to represent what a percentage is – how the percentage relates to the height.
Diagnostic and formative information: 
  Common error Likely calculation Likely misconception
a) i)
    ii)		 50
25		   Writes percentages as actual heights
Does not understand that a percentage indicates a part of the whole 100%. Treats percentage as a whole number.
a) i)
    ii)		 25 or 20
15 or 10		 subtracts off 5,10,15, etc Adjusted down
Doesn't have a proportional recognition of the relationship between the height and the percentage and reverts to an additive strategy.
a) ii) 7 or
7 and a "bit"
(71/7 , 7.1, 7R1)		 Attempts to halve 15 Lacking decimal understanding
Cannot halve 15 accurately (possibly because of decimal), but recognises that 7 and some small part is close enough.
a) ii) 5 or 10 Attempts to halve 15 Lacking decimal understanding
Recognises 50%, but cannot halve 15 (reverts to factors of 5).

Strategies
Finding 50% and 25%
Most students answered questions a) i) and ii) by using successive halving to find 50% and 25%.
Some students also found the heights by finding the mid-point between the heights of interest, e.g., 50% is midway between 0 and 30 (15 metres), and 25% is midway between 0 and 15 (7.5 metres). 

Finding 75%
The most common strategy described by students either explained adding 25% to 50% or used the specific amounts from the resources, i.e., adding 15 to 7.5.  A small number of students described 75% as half way between 50% and 100%, and some backed this up with a measurement using a ruler.  A very small number of students multiplied 25% by 3 to get 75%.

Next steps: 

Students who adjusted down in some way or subtracted estimates from the total height, or students who wrote the percentages as the actual heights may not understand that the percentages are a proportion of the height of the building.  They may have had no experience relating percentages to actual values as in this diagram.  The double number line is a tool that can be used to solve percentage problems by representing partitioning and recombining of the parts (e.g., partitioning into quarters and combining three parts to make 75%).  Students will need to be aware what 100% and 50% represent and that whatever happens with the percentages affects the height in the same way.
Students could be asked what 50% of the height is (if the building is 20 metres high), then 25%, and 75%.  Many students at this level will be aware of successive halving as a strategy, but may need help with decimals (from halving odd numbers), and building up 25% units to make 75%.

Lacking decimal understanding
Students who halved 15 to get 7 (or "7 and a bit") may need to justify how half of 15 can be 7 and try to find a more accurate way of working out "what the bit left over is".  More exploration finding half of an odd number would also support students with this misconception (and for students who answered 5 or 10 for this question).

Further exploration
Students who can identify the 25%, 50%, and 75% could either look at finding 12.5, and 6.25% (continued halving).  They could also explore the idea of "tenthing" needed to find 10%.  This may involve them re-thinking what the best way is to break down the total (beyond halving).  Ask questions like "how many 10% in 100%?" combined with "what goes into 20 metres ten times?" 
10% requires students to partition the total into a different number of parts (other than halving with which they are more familiar), or recognise the 10% as a known part, i.e., that 10% (or 1/10) of 20 is 2.

 
 
Links to the Number Framework
Working with percentages and simple double number lines can involve working with a halving strategy for which students may need to be at the Early additive part-whole stage of The Number Framework (Book 1) strategies.
 
 
 
Numeracy resources
Book 7: Teaching Fractions, Decimals and Percentages, 2006
Seed packets, (p.17), Early additive part-whole / Advanced additive part-whole.