How many groups?
a) There are 21 Easter eggs. Show how to work out how many baskets of 3 eggs can be made.
|
|
|
b) 40 apples are given out equally so people so have 8 each. Show how to work out how many people there are.
|
|
|
c) There are 4 cookies in a packet. Show how many packets can be made from 32 cookies.
|
|
|
d) There are 60 sweets. Show how many piles of 5 sweets can be made.
|
| Y4 (11/2007) | ||
| a) |
7 Working that can involve:
|
easy easy |
| b) |
5 Working that involves any of the above strategies, i.e.: writing the problem as a division equation; reverse multiplication; skip counting; repeated addition; or drawing a diagram (array, quotitive diagram, or a partitive diagram). |
moderate moderate |
| c) |
8 Working that involves any of the above strategies, i.e.: writing the problem as a division equation; reverse multiplication; skip counting; repeated addition; or drawing a diagram (array, quotitive diagram, or a partitive diagram). |
moderate moderate |
| d) |
12 Working that involves any of the above strategies, i.e.: writing the problem as a division equation; reverse multiplication; skip counting; repeated addition; or drawing a diagram (array, quotitive diagram, or a partitive diagram). |
moderate moderate |
Based on a representative sample of 250 students.
Why quotition?
The distinction between quotitive and partitive division becomes important when students are asked questions like 2 ÷ 1/2. If they only have experience with the equal sharing model of division they will try to equally share 2 between a half (which may not make much sense to them), whereas if they could say "how many 1/2s in 2?" the problem is more accessible. It is important to give students a range of experiences with these different aspects of division to develop a fuller understanding of division, including the inverse relationship with multiplication (multiplicative inverse).
This resource involved quotitive division which is less easily recognised as division than partitive division - which may explain why fewer students used multiplicative strategies (18% across the 4 questions). The most common strategies for all questions were quotitive diagrams of grouped sets (30%), multiplicative (18%), and repeated addition (8%). Approximately 15% did not show their working. About a third of the students who showed no working but gave an answer got it correct.
The most common successful strategy (proportion of correct answers for that strategy) across all four questions was skip counting (92%), followed by reverse multiplication and recognising the questions as a division (both 90%). Division working could be shown in either form:
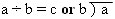
Students who used repeated addition and those that drew quotitive diagrams to solve the problem both averaged 78% success. Students who drew quotitive diagrams resulted in more correct answers than partitive diagrams (30% success). A partitive diagram does not represent the problems in this resource, e.g., 21 eggs in baskets of 3 would be 7 baskets of 3. A partitive diagram that a small number of students drew was 3 baskets of 7 eggs.
| Common error | Likely misconception | |
|
a) b) c) d) |
24 (or 18) 48 (or 32) 36 (or 28) 65 (or 55) |
Using an incorrect operator (10% of responses) Students add (or subtract) the numbers. Addition tended to be the more common operator used. Underneath this error is likely to be a reading error. Students may not have seen quotitive problems before. |
|
a) b) c) d) |
6 or 8 4 or 6 7 10/11 |
Out by a factor error Students give an answer that is 1-2 counts away from the correct solution. |
|
a) b) c) d) |
3 lots of 7 8 lots of 5 4 lots of 8 5 lots of 12 |
Not representing the maths problem correctly Although the use of a partitive diagram should yield the correct answer, it is reversing the number of groups and the number within a group. and therefore doe not accurately represent the problem. |
|
a) b) c) d) |
3 8 4 5 |
Writing down the factor already given Students may solve the problem but write down the same factor they have been given in the question. |
For students who use an incorrect operator get them to draw or explain the story problem, e.g., "If each person gets 4 pieces of chocolate and there are 36 pieces, how could we show that?". Use simpler numbers and/or materials to illustrate and encourage students to be able to justify their working. Get students to create their own story problems (mathematical problem writing) using all four operations to help them recognise how the operations sound in story problems, e.g., the resource Writing word problems for all operations or Making number sentences and Making number sentences II (for multiplication and division) or use the keyword, story problems.
Out by a factor error
Students who indicated this error used diagrams, repeated addition, skip counting, or did not show their working. Checking over their working and explaining how their working relates to the problem should reveal the "miscount".
Students draw a partitive diagram to represent the situation
A partitive diagram would be regarded as an incorrect representation of the relationship for these division questions. For example, for question a) a partitive diagram would look like 3 lots of 7 (21 being shared out into 3 groups):
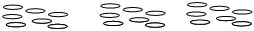
However these quotition division questions ask how many groups if there are 3 in a group. This would look like 7 lots of 3 (with 7 being the unknown):
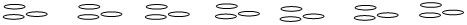
Encourage students to explain how their diagram relates to the scenario. Help them to realise that division can be represented in different ways (quotition, partition), and that with a context the numbers can represent the number of groups to divide into (divisor), the number in each group (quotient), or the total number of objects (dividend).
Reversing the division expression (divisor ÷ dividend)
For students who write the division in the incorrect order (i.e., 3 ÷ 21 = 7) ask them to read back the number sentence using the word "divided by" for division (as opposed to "goes into"). This error is a mathematical communication error rather than a computational one.
Using diagrams to show working
Students who use diagrams to show how to solve these questions should be encouraged to work towards visualising the problem and trying to solve it in their head.
Writing down the factor already given
For students who write the same factor they have been given in the question as the answer, it is likely they are getting the two factors confused. Encourage them to devise a method to check their answer.
Links to the Number Framework
The strategies that students use can determine their stage of development within the Number Framework. Strategies that could be used for this resource include counting out, one-to-one mapping, visual grouping, partitioning and trial and error, repeated addition/subtraction, skip counting, multiplication, and division. Students using repeated addition are indicating Stage 5 (Early additive) strategies, and students using multiplicative strategies are indicating Stage 6 (Early multiplicative).
- Stacking wood
- Buying books
- Counting sheep
- Numbers at an art show
- Cough medicine
- Cans of fruit drink
- Dividing with remainder
- No remainder
- Give-aways
- Packing cherries
- Sharing fruit and vegetables
- Division wheel
- Calculating with time
- Writing word problems
- Sharing Jelly beans
- Town hall concert
- Division
- Working with numbers II
- Money computations
- Multiplying and dividing fractions
- The price of flour
- Shopping for vegetables
- Estimating cards, money and pinecones
- Equal sharing II
- Equal sharing III
- How many groups? II
- Powerful twenty five
- How many are there?
- Sharing out
- Christmas
- Saving money
- Buying a phone
- Anahera's sweets




