Who is using what social media

Who is using what social media

Auto-markingPencil and paperOnline interactive
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about interpreting data from a bar graph.
Age of people who use social media
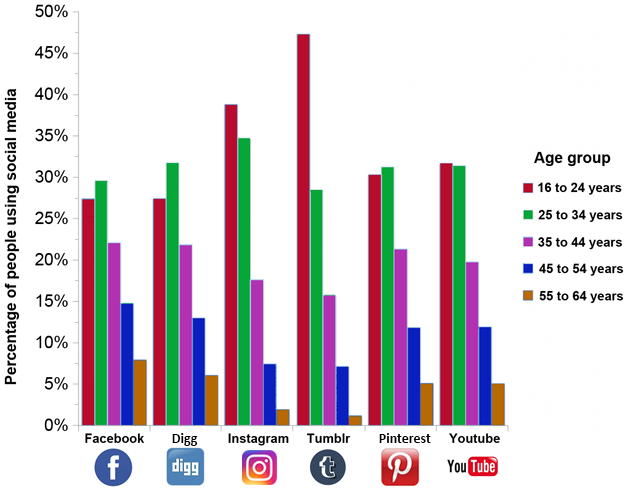
social-media-graph-500.png
A survey was done to find out what social media applications different age groups used. The results are shown on a graph above.
Use this graph to answer the following questions.

Question 2Change answer

a)  What percentage of 55-64 year olds used YouTube?  %

Question 2Change answer

b)  What percentage of 16-24 year olds used Digg?  %

Question 2Change answer

c)  What percentage of 35-44 year olds used Instagram?  %

Question

d)  What is the most popular social media application for 16-24 year olds?

    • facebook.png

    • google-plus.png

    • instagram.png

    • tumblr.png

    • pinterest

    • youtube.png

Question

e)  What is the most popular social media application for 25-34 year olds?

    • facebook.png

    • google-plus.png

    • instagram.png

    • tumblr.png

    • twitter.png

    • youtube.png

Question

f)  What social media has the largest difference between the oldest and youngest age groups? 

    • facebook.png

    • digg

    • instagram.png

    • tumblr.png

    • pinterest

    • youtube.png

Question

g)  What social media application has the smallest difference between the oldest and youngest age groups? 

    • facebook.png

    • digg

    • instagram.png

    • tumblr.png

    • pinterest

    • youtube.png

Task administration: 
This task can be completed with pencil and paper or online (with auto marking displayed to students).
Level:
4
Curriculum info: 
Maths, Statistics, Statistical investigations
Keywords: 
graph interpretation, bi-variate data, graphs, bar graphs
Description of task: 
Students interpret bi-variate data on a bar graph to answer questions about social media and age of users.
Curriculum Links: 
This resource can be used to help to identify students' ability to interpret bar graphs with bi-variate data.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Statistical investigations, set 5
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
  Y7/8 (03/2017)
a) 5% very easy
b) 27.5% very easy
c) 17.5% easy
d) tumblr.png very easy
e)
 instagram.png very easy
f) tumblr.png very easy
g) facebook.png very easy
Based on a sample of 40 Y7-8 students.
Diagnostic and formative information: 
  Common error Misconception
b)
c)
25.5
15.5
Incorrect interpretation of unlabelled mark on y-axis
Student treats the next unlabelled mark from 25 as "half" (0.5) not 2.5.
b)
c)
26
16
 Student treats the next unlabelled mark from 25 as "one" (0.5) not 2.5.
b) 
c)
28
18
Reads value of unlabelled mark incorrectly
Student follows the line across to the y-axis accurately, but uses the incorrect value of the unlabelled mark.
or
Not following a straight line from the data to the scale on the y-axis
Student doesn't follow the line from the data on the graph to the y-axis accurately,
f) and g)
 
facebook.png tumblr.png
Not finding the smallest and largest difference correctly
Students identify the application that has the largest or smallest use rather than the largest or smallest "difference".
Next steps: 
Incorrect interpretation of unlabelled mark on y-axis
Students who read the unlabelled mark as 0.5% or 1% rather than 2.5%, could be asked to identify and write down all the values on the graph. They could check the y-axis scale to make sure the intervals are equal sized, and discuss how all of the values on the axis must be consistent (in a linear scale).
 
Not accurately following a straight line across from the data to the scale
Students who may have inaccurately worked out the line as they moved across from the data in the graph to the scale on the y-axis could use a ruler or any straight-line object to guide their eye straight across, and then re-check going back the other way.
 
Not finding the smallest and largest difference correctly 
Students who didn't find the smallest/largest difference, may simply need to explore the meaning of difference, and what a small and large difference mean (and look like). As a simple comparison they could be asked to focus on the first two age groups on the graph and compare them to find the difference.
Are they more or less? How much more? (this is the difference)
Once they have a sense of "difference", get them to look for an application with the largest difference, and then the smallest difference.