Going on camp

Going on camp

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about showing how to solve story problems.

Three classes from Wainui school are at a two-day camp.

a) At the camp there are 25 boats, but 8 have holes in them and can't be used. Show how to work out how many boats can be used.

 
 
 
 

Answer: __________  

b) 47 buns are taken on camp.  On the first day 15 buns are eaten. Show how to work out how many buns are left for the next day.

 
 
 
 

Answer: __________  
 
c) 65 students are on camp.  If 29 of them go on a walk, show how to work out how many students are left at camp.
 
 
 
 

Answer: __________  

d) Two camp teams play cricket. Red team get 104 runs and Green team get 46 runs. Show how to work out how many more runs Red team got.

 
 
 
 

Answer: __________  
Task administration: 
This task is completed with pencil and paper only.
Levels:
2, 3
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Key Competencies: 
Using language, symbols, and texts
Keywords: 
subtraction
Description of task: 
Students solve subtraction story problems and show their strategies.
Curriculum Links: 
This resource can help to identify students' ability to use basic facts and knowledge of place value and partitioning whole numbers to solve subtraction problems. Some of the strategies for these are:
  • Partitioning using rounding and compensation strategies (Number Framework Stage 6 - Advanced Additive).
  • Place value partitioning using tens and ones (Number Framework Stage 5 – Early Additive).
  • Place value partitioning expressing tens as ones (Number Framework Stage 5 – Early Additive).
  • Using counting-on (Number Framework Stage 4 – Advanced Counting).
  • Using counting all (Number Framework Stage 3 – Counting from One).
Key competencies
This resource involves recording the strategies students used to solve subtraction problems. This relates to the Key Competency: Using language, symbols and text.
For more information see http://nzcurriculum.tki.org.nz/Key-competencies.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Additive thinking, set 5
Additive thinking, sets 6-7
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
    Y4 (11/2007)
a) 17
Working that involves subtraction of 8 from 25:

  • Place value partitioning, e.g., 20 – 8  + 5
  • Derived place value partitioning:  25 – 5 – 3
  • Vertical algorithm (working form)
  • Accumulated addition: 9 + 56 = 65, 65 + 72 = 130 + 7
  • any other working that involves the correct operation (addition), all the numbers, and is complete.
 easy
moderate
b) 32
Working that involves any of the above strategies and the subtraction of
47 – 15		 moderate
moderate
c) 36
Working that involves any of the above strategies and the subtraction of
65 – 29		 difficult
moderate
d) 58
Working that involves any of the above strategies and the subtraction of
104 – 46		 very difficult
difficult

Based on a representative sample of 273 Y4 students.

Teaching and learning: 
This resource explores the strategies students use to solve subtraction problems.  In the context of the classroom these would be shared back, and students would discuss and critique the best, fastest, easiest, or most efficient strategies.

Links to the Number Framework
Subtracting numbers involving recombination is at the Early/Advanced additive part-whole stage (Stages 5-6) of the Number Framework.

Diagnostic and formative information: 
Strategies
The most common strategies used were part-whole strategies such as place value partitioning (15% across all questions) followed by tallying or marking out a visual representation of the numbers and crossing out or marking the number subtracted (subtrahend) from the initial total (minuend) (15% for questions a, b, and c).  This latter strategy decreased notably when the numbers became too large to represent or count.

For question d) the most common strategy involved complementary addition or reversibility (Don't subtract – Add, Early/Advanced additive part-whole, Book 5: Teaching Addition, Subtraction, and Place Value, 2007) where a subtraction problem is reversed to become an addition problem, e.g., 104 – 46 = ? becomes 46 + ? = 104.  This strategy was rarely used for the other questions.  Just over 5% of students used the vertical algorithm (working form). A quarter of students simply wrote their working as a subtraction equation – these students were more successful than students who made no attempt to show any working yet gave an answer.

The most successful strategies (that led to correct answers) were place value partitioning (70%), followed by the vertical algorithm (68%).  Other part-whole strategies involving tidy numbers and compensation were evident, but the compensation was applied incorrectly for a number of examples. As the numbers got larger the counting and visual strategies became less successful (from 85% down to 29%) for solving for the correct answer.

  Common error Likely misconception
d) 150 Incorrect operator
Students added the numbers instead of subtracted.
c)
d)		 44
62		 Over generalising ("won't go") error
Students may swap the subtrahend (number being subtracted) and the minuend (number being subtracted from) to subtract the smaller number from a larger number. For example in the problem 65 – 29, students might attempt to subtract 9 from 5, but when that doesn't go, they will subtract 5 from 9 to get 4, and then 60 – 20 = 40, è 44.
a)
b)
c)
d)		 16, 18
31, 33, 34
34, 37
54, 60		 Calculation  error
Students made a calculation error of the digits and their answer was out by a small amount.
NOTE: About 10% of students made this error.
c)
d)		 46
68		 Place value error
Students did not account for recombining the ten that was partitioned to "borrow" for the ones subtraction, i.e., the ten was borrowed by the ones, but not accounted for by reducing the number of tens by one.
c)
d)		 45
62		 Combination of won't go and calculation error
Student swapped the ones to subtract the smaller number from the larger number and then made a calculation error.
Next steps: 
Incorrect operator
For students who used the incorrect operator and added the numbers, get them to describe what is actually happening in the maths problem and use materials to explore what to do with them to represent the problem.

Computational error  
Students who made simple calculation errors could be encouraged to check over their subtraction and look at how they are developing their working to find the answer. Basic facts are an important part of developing the strategies to solve problems. Students may need to explore the part-whole additive strategies they use when subtracting from numbers under 20.  After developing this understanding students should describe how to solve subtraction problem with "recombination" or borrowing (see Place value error).

Place value error
Students who don't take into account the need to compensate when "borrowing" a ten may need to explore what happens when numbers are subtracted from each other involving recombination, i.e., indicate what a subtraction can look like with abacus, place value blocks, tens frames, etc. 
For example, students could use an abacus to show what happens when we subtract 29 from 65.
At some stage we want to take 9 away from 5 and will need to work out how to do this (borrowing, renaming, splitting numbers into parts, or some other way).

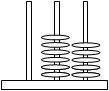
For those students who successfully subtract the numbers have them check the reasonableness of their work, by estimating the size of the answer (Estimation as a Check, Book 5: Teaching Addition, Subtraction, and Place Value). Additionally, students could look at constructing their own maths problems (Mathematical problem writing).

Numeracy Project Resources
Book 5: Teaching Addition, Subtraction, and Place Value, 2007
  • Subtraction in parts (Early additive part-whole)