Solving more maths problems
 |
||
| a) | There are 28 people at a picnic, and 12 people leave. Show how to work out how many people stay at the picnic. | |
|
||
| b) | A train has 65 people on board, and 27 get off. Show how to work out how many people stay on the train. | |
|
||
| c) | Devon has 85 flowers to make lei. She gives 39 of them to her friend. Show how to work out how many flowers she still has. | |
|
||
This resource can help to identify students' understanding of subtraction. Students' strategies give a much better indication of the curriculum level and progress than their answer. A possible progression for understanding could involve using
- only counting-back strategies (Number Framework Stage 4 - Advanced Counting).
- place value partitioning with tens as ones (Number Framework Stage 5 - Early Additive). The student recognises the role of tens and ones but cannot use them to compensate or cross the tens boundary correctly.
- place value partitioning with tens and ones and incorrect compensation (Number Framework Stage 5 - Early Additive). The student recognises the role of tens and ones but cannot use them to compensate or cross the tens boundary correctly.
- place value partitioning with tens and ones and consistent correct compensation (Number Framework Stage 5 - Early Additive).
- place value partitioning with tens and ones and correct compensation involving negative numbers. Negative number do not arise until curriculum level 4, but some students show readiness for them earlier.
- partitioning using rounding and compensation strategies (Number Framework Stage 6 - Advanced Additive).
Incomplete strategy use that results in a correct answer may indicate the student is operating at an early point of the relevant Number Framework stage. Students who just give an answer, or who make statements such as "28 - 12 = 16" need to be questioned how they got their answer, and then levelled according to the table above.
| Y5 (05/2010) | ||
| a) |
16 Any 1 of:
|
moderate |
| b) |
38 Any 1 of the above strategies (partitioning, place value, counting etc.), including evidence they can correctly cross the tens boundary such as the methods below.
|
difficult |
| c) |
46 |
difficult |
NOTE:
- Students who use a correct strategy but do not get the correct answer due to a minor error still gain credit for their working. Often students do not compensate correctly in subtraction situations.
- Students using the vertical algorithm should be asked how and why it works to see if it is just procedural knowledge rather than displaying understanding. This is just one way of solving subtraction, and should only be explored after students have explored their own strategies for solving such problems.
Student strategies
- The strategy that led to the correct answer most often was Partitioning using rounding and compensation to cross boundaries (partitions across boundaries). This was also used by students with the second highest mean ability.
- Partitioning by rounding to a tidy number then compensation (Partitions with nice numbers) was used by students with the highest mean abilities, but was a little less successful than the above strategy.
- Place value partitioning using tens and ones (PV partitions with 10s and 1s) was used by the next most able group of students, but was only successful just over 50% of the time. This was because large numbers of students made errors in applying it, especially in parts b) and c). They often did not use renaming correctly or used a "won't go" strategy on the ones digit.
- Students using the Vertical algorithm were less able that those using all the above strategies, but more likely to lead to a correct answer than students using place value partitioning in tens and ones.
- Students who used Place value partitioning expressing tens as ones had about a 50% success rate part a) but virtually never got parts b) and c) correct.
- Visually displaying partitioning or Other PV strategies were of a typical mean ability and had a success rate close to 50%.
- Students who restated the problems or gave the subtraction equations "28 - 12 = 16" were typical mean ability. They often got part a) correct, but were far less successful in parts b) and c).
- Students using counting strategies were of low mean ability, and were rarely successful.
- Students with incomplete strategies had a typical mean ability, but had low success rates.
- Students who did not show any working had the second lowest mean abilities, and had very little success on parts a) - c).
| Common response | Likely computation | Likely misconception | |
|
a) b) c) |
40 92 124 |
28 + 12 65 + 27 85 + 39 |
Adds the numbers instead of subtracting them Students do not comprehend the problem or may not have read it carefully enough. Their answer can show whether they have correct addition strategies, and how sophisticated these are. |
|
a) b) c) |
30 82 114 (or 1114) |
20 +10 + 0 60 + 20 + 2 80 + 30 + 4 |
Adds the numbers without "carrying" instead of subtracting them These students do not correctly take account that the ones digits sum to more than 10 and hence get an answer that is too small by 10. While this is often associated with the vertical algorithm, it also occurs with partitioning strategies. |
|
a) b) c) |
14, 15, 17 or 18 36, 37 or 39 44, 45, 47 or 48 |
Miscounts by 1 or 2 The student is using a counting strategy but miscounts by a small amount. It also occurs with students who use part-whole partitioning strategies, suggesting that these students were using counting strategies for the ones. |
|
|
b)
c)
|
42
54
|
60 - 20 = 40 7 - 5 = 2 40 + 2 = 42
80 - 30 = 50 |
Over generalising ("won't go") error Students swap the subtrahend (number being subtracted) and the minuend (number being subtracted from) when they subtract the smaller number from a larger number. For example in the problem 65 - 27, students might attempt to subtract 7 from 5, but when that doesn't go, they will subtract 5 from 7 to get 2, and then 60 - 20 = 40, → 42. This was by far the most common error, and occurred nearly half the time when students used place value partitioning. It was less prevalent with the vertical algorithm than with place value partitioning even though it is most often associated with the former |
|
b)
c) |
48 (or 28)
56 (or 36) |
60 - 20 = 40 15 - 7 = 8
80 - 30 = 50 |
Place value error - Crosses the tens boundary without "renaming" The student does not compensate for performing 15 - 7 instead of 5 - 7 . The student gets an answer ten more (or occasionally less) than the correct answer. This happened often with place value partitioning but did not occur with any students using the vertical algorithm. It was reasonably uncommon in b) and c), but did not occur in part a). |
|
b)
c) |
40 (or 30)
50 |
60 - 20 = 40 5 - 7 = 0
80 - 30 = 50 |
Failure to cross the tens boundary The student recognises how to correctly subtract the ones, but does not know what to do when the subtrahend (number being subtracted) is larger that the minuend (number being subtracted from) and assumes the result is 0. |
Adds the numbers instead of subtracting them
These students may have a made a reading error. Get them to describe what is actually happening in the maths problem. They need to see that the initial amount (minuend) is being reduced by taking away a number of objects (the subtrahend). They may initially need to use materials to explore what to do. Information about these students' adding skills can be gained from looking at their answers and the strategies they used.
Miscounts by 1 or 2
Students who used just counting back strategies could be encouraged to start to explore the part-whole additive strategies they use when subtracting from numbers under 20. This is referred to as complimentary addition or reversibility. After developing this understanding students should describe how to solve a subtraction problem with "recombination" or borrowing (see Place value error), or use number lines.
Students who use part-whole partitioning strategies coupled with counting strategies for the ones need to work on their subtraction basic facts. These are an important part of solving problems by removing the reliance on strategies that are at earlier stages of the Number Framework.
Over generalising ("won't go") error
Students could be exposed to some problems where this strategy clearly leads to a wrong answer. Good examples would be 65 - 57 or 85 - 79. Both must be single digit answers, but these students' strategies would lead to 12 and 14 respectively, which are both too large. The ones digit is also incorrect. They could solve these examples by counting back, or solve the equivalent problems 57 + = 65 or 79 + = 85 by counting on. The students could then draw these on number lines, then incorporate the tens to do the original problems. The resources Alternatively, they could work with the "renaming" ideas below.
Place value error - Crosses the tens boundary without "renaming"
Students who don't take into account the need to compensate when "borrowing" a ten may need to explore what happens when numbers are subtracted from each other involving recombination, i.e., indicate what a subtraction can look like with abacus, place value blocks, tens frames, etc.
For example, students could use an abacus to show what happens when we subtract 27 from 65.
At some stage we want to take away from 5 and will need to work out how to do this (borrowing, renaming, splitting numbers into parts, or some other way). These students could also work with problems representing them on number lines.
If the student was using place value partitioning, then they could decompose 65 - 27 (for example) as (50 + 10 - 20) + (5 - 7) = (50 - 20) + (10 + 5 - 7) = 30 + (15 - 7). This shows 60 renamed as 50 + 10 and then regrouping (commuting) the numbers.
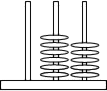
Failure to cross the tens boundary
Students who do this are ready for the concept of negative numbers, so instead of stopping at zero, they can see that 5 - 7 = -2. This is best done on a number line that is extended to the left into negative numbers. Once they have grasped this, they should explore how to compensate with the -2.
Successful students
For those students who successfully subtract the numbers have them check the reasonableness of their work, by estimating the size of the answer (Estimation as a Check, Book 5: Teaching Addition, Subtraction, and Place Value). These students will typically be those performing above Level 2 of the curriculum. Additionally, students could look at constructing their own maths problems (Mathematical problem writing).
Numeracy Project Resources
Subtraction in parts (Early additive part-whole), Book 5: Teaching Addition, Subtraction, and Place Value, 2007
- Buying groceries
- Numbers at an art show
- Bank account
- Cans of fruit drink
- Temperature changes
- City populations
- How much farther?
- Addition wheel
- Subtraction wheel
- Showing change
- Adding and subtracting
- Change from $10
- Lemons, library and sports
- Spending pocket money
- Working out change
- How much change?
- Writing word problems
- Keep fit programme
- Sharing Jelly beans
- Bear mixes
- Fractions
- Money computations
- Adding and subtracting fractions III
- At the canteen
- Student answers
- Number line addition and subtraction III
- Cover up
- Seeds and sweets
- Number line subtraction II
- Number line subtraction
- Number line addition and subtraction
- Eating fractions of pie, pizza and cake
- Cover up II
- Going on camp
- Fractions of cake
- Buses, games and trains
- Easy or harder subtractions
- Collecting beads
- Party balloons
- Adding and subtracting more numbers
- Going on a picnic
- Spending at the shop
- Buying some things
- Making a cake
- Fruit and vegetables
- Buying a phone

